по быстрее как можно скорее. Мне нужно
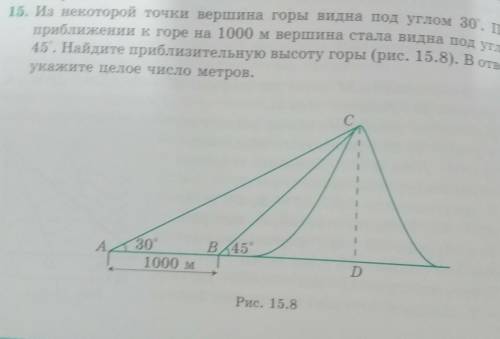
Из некоторой точки вершина горы видна под углом 30 градусов приближение Карина 1000 м вершина стала видна под углом 45 градусов Найдите приблизительно высоту горы в ответе Укажите целое число метров
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.В равнобедренном треугольнике основание 2 м, а боковая сторона 26 дм. Найдите...
3 - Сейчас нужно и Лучший ответ! Составьте предложения:1. Her, is, than, house,...
3 - 2. Прочитайте текст. Выделите смысловые части, озаглавьте касдую на тих, Сделайте...
1 - 1. Какие государства находились на ближнемВостоке? 2.Формаправления в данныхгосударствах?...
2 - Ғылым таппай мақтанба өлеңінің фабуласып жазып,шығармада көтерілген мәселені...
3 - Какую оценку дает автор Онегину в первой главе? Укажите один или несколько...
3 - Найди словосочетание с самостоятельным местоимением это страна моя страна страна...
1 - В сосуде содержится смесь льда и воды, находящуюся при температуре 0 °С. Масса...
2 - Орындау уақыты Тапсырма1. «Мен жазбаймын өлеңді ермек үшін» шығармасында қандай...
1 - Сколько АТФ и энергии в кДж выделиться при бескислородном разложении 7 молекул...
1
1. В задаче мы имеем два треугольника - треугольник ABC и треугольник ACD. Треугольник ABC представляет гору, а треугольник ACD представляет приближение Карины к горе.
2. Для начала, обратим внимание на то, что у нас даны два угла (30 градусов и 45 градусов) и одна сторона (1000 метров).
3. Мы можем использовать тангенс углов, чтобы найти длину других сторон треугольника. Также обратим внимание, что угол между стороной, видимой под разными углами, будет одинаковым.
4. Применим теорему синусов к треугольнику ABC:
sin(30 градусов) = высота горы / сторона BC
5. Заменим sin(30 градусов) на его численное значение (0.5):
0.5 = высота горы / сторона BC
6. Так как у нас нет информации о стороне BC, нам нужно найти ее. Для этого мы можем использовать теорему синусов в треугольнике ACD:
sin(45 градусов) = высота горы / сторона AC
7. Заменим sin(45 градусов) на его численное значение (0.7071):
0.7071 = высота горы / сторона AC
8. Мы знаем, что сторона AC равна 1000 метров (дано в задаче), поэтому заменим это значение:
0.7071 = высота горы / 1000
9. Для решения этого уравнения относительно высоты горы, умножим обе стороны на 1000:
0.7071 * 1000 = высота горы
10. Рассчитаем значение:
высота горы = 707.1 метров
Ответ: Ответом будет приблизительная высота горы, равная 707 метрам.