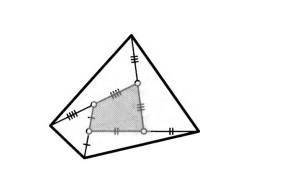
Площадь закрашенного четырехугольника равна 1. Все его стороны продолжили на свою длину так, как это показано на ри­
сунке. Найдите площадь получившегося большого четырехуголь­
ника.​

Добрый день! Я рад быть вашим школьным учителем и помочь вам решить эту задачу.

Давайте разберем пошаговое решение задачи:

1. Вначале посмотрим на рисунок и обратим внимание, что у нас есть четырехугольник с известной площадью, которая равна 1.

2. Заметим, что после продолжения всех сторон четырехугольника получится большой четырехугольник.

3. Чтобы найти площадь большого четырехугольника, нам нужно найти длины его сторон.

4. Рассмотрим каждую сторону по отдельности:

- Первая сторона четырехугольника, продолженная, образует правильный шестиугольник. Так как площадь первоначального четырехугольника равна 1, то площадь этого шестиугольника также равна 1. Расположим шестиугольник в вертикальном положении и обратим внимание, что он состоит из 3 равносторонних треугольников.

- Третья сторона четырехугольника также продолжается и образует еще один равносторонний треугольник.

- Вторая и четвертая стороны четырехугольника продолжаются и формируют прямоугольник, который можно разделить на два равных параллелограмма.

5. Теперь, когда у нас есть информация о длинах всех сторон большого четырехугольника, мы можем найти его площадь.

6. Площадь большого четырехугольника можно получить сложив площади каждой его части, то есть шестиугольника, треугольника и двух параллелограммов.

- Площадь шестиугольника можно найти как площадь треугольника, умноженную на 6. Так как шестиугольник состоит из 3 равносторонних треугольников, площадь шестиугольника будет 6 раз больше площади одного треугольника.

- Площадь треугольника можно найти используя формулу площади равностороннего треугольника, которая составляет s^2 * sqrt(3) / 4, где s - длина стороны треугольника.

- Площадь параллелограмма можно найти, используя формулу площади, которая составляет основание * высоту. В нашем случае, длина основания параллелограмма равна длине стороны четырехугольника, а высота равна длине третьей стороны четырехугольника.

- Сложим все полученные площади, чтобы найти площадь большого четырехугольника.

7. Подставим значения длин сторон, которые мы нашли ранее, в формулы для расчета площадей частей большого четырехугольника и выполним все необходимые вычисления.

8. В результате получим площадь большого четырехугольника.