Площадь сечения шара плоскостью отдаленной от ее центра на 4 см равна 25 пи см^2 найдите площадь поверхности шара
Другие вопросы по теме Геометрия
Популярные вопросы
- Ежик выехал из москвы в 9 утра 20 февраля а приехал в тюмень в 9 часов вечера...
1 - Переведите вопросы: -большой ли у клер котёнок? -какого цвета его лапки,хвост,уши?...
2 - Ойлан тап тапсырмасы: булдозерді, экскаваторды, мұнара -кранды, тікұшақты жүргізетін...
1 - Уповерхности воды мальчик выпускает камень, и он опускается на дно пруда на...
2 - Док-ва или опровержения,что завоевание в 1066 году ускорило процесс объединение...
3 - Вгруппе из 100 туристов 70 человек знают язык, 45 знают французский язык, из...
3 - Подбери подходящие местоимения.запиши.определи их лицо. а ненасытный птенец...
2 - Посчитать с учетом сложного и простого процента сумму кредита, если вы взяли...
1 - Укапусты в каждой соматической клетке содержится по 18 хромосом. сколько хромосом...
2 - Как слепой красный топает надулся нем...
2
Т.к. сечением является круг, его радиус найдем как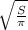 (исходя из формулы
(исходя из формулы 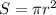 .
. 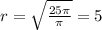 (см). Расстояние от плоскости сечения до центра шара, радиус сечения и радиус шара образуют прямоугольный треугольник. Его гипотенузу (радиус шара) вычислим по т. Пифагора:
(см). Расстояние от плоскости сечения до центра шара, радиус сечения и радиус шара образуют прямоугольный треугольник. Его гипотенузу (радиус шара) вычислим по т. Пифагора:
ответ: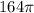 см^2.
см^2.