1. Геометрия
  2. Площадь ромба равна 100 см²,

Площадь ромба равна 100 см², а острый угол равен 30°. Найти диагонали d1 i d2 ромба. Решение должно быть 10(√3+1) и 10(√3-1) см

sPHAgNUM1 sPHAgNUM1    1   02.12.2021 01:46    1

Ответы
Маша270902 Маша270902  13.01.2022 15:15

d_1=10(\sqrt{3} -1), d_2=10(\sqrt{3}+1)

Объяснение:

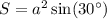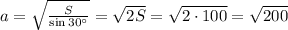Для начала найдем сторону ромба по формуле S=a^2 \sin (30 ^\circ) имеем a=\sqrt{\frac{S}{\sin {30^\circ}} }=\sqrt{2S}=\sqrt{2 \cdot 100}=\sqrt{200}. Так как диагонали ромба лежат на биссектрисах его углов, то прямоугольный треугольник образованный половинами диагоналей и стороной будет иметь угол 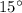15^\circ. Причем гипотенуза его равна 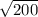\sqrt{200}, а катеты половины диагоналей.

Имеем формулы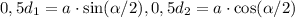 0,5d_1=a \cdot \sin(\alpha/2), 0,5d_2=a \cdot \cos(\alpha/2). Где α острый угол между двумя сторонами ромба. Осталось посчитать 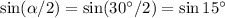\sin (\alpha/2)=\sin (30^\circ/2)=\sin 15^\circ подставить в формулу.

\sin 15^\circ=\sqrt{(\sin 15^\circ)^2} =\sqrt{\sin^2 15^\circ} =\sqrt{ \frac{1-cos(2 \cdot 15^\circ)}{2}} =\sqrt{ \frac{1-cos(30^\circ)}{2}} =\sqrt{ \frac{1-\frac{\sqrt{3}}{2} }{2}}=

=\sqrt{ \frac{1-\frac{\sqrt{3}}{2} }{2}}=\sqrt{ \frac{2-\sqrt{3}}{4}}= \frac{\sqrt{2-\sqrt{3}}}{2} .

Далее имеем:

0,5d_1=a \cdot \sin(\alpha/2)=\sqrt{200} \cdot \frac{\sqrt{2-\sqrt{3} }}{2} =5(\sqrt{3}-1) ⇒ d_1=10(\sqrt{3} -1)

0,5d_2=a \cdot \cos(\alpha/2)=\sqrt{200} \cdot \frac{\sqrt{2+\sqrt{3} }}{2} =5(\sqrt{3}+1) ⇒ d_2=10(\sqrt{3}+1)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
realranktest realranktest  21.04.2020 14:45
Основи рівнобічної трапеції дорівнює 5см і 11 см, а її висота 6 см. Знайдіть діагональ трапеції.​...
VAI81416 VAI81416  21.04.2020 14:45
Знайти площу ромба,сторона якого 15 см,а одна з діагоналей 24 см.​...
ibrashovo ibrashovo  21.04.2020 14:44
Побудувати ГМТ, різновідаленних від двох даних паралельних прямих.​...
DANIL79NR DANIL79NR  21.04.2020 14:44
Определите вид треугольника BCD и длину его медианы DM, если B(0, 2), C(6, 4), D(5, -3)​...
ariiiiiaha ariiiiiaha  08.11.2020 08:10
Чему равны стороны прямоугольника a и b, если они соотносятся как 5 : 3, а площадь прямоугольника равна 960 дм2? Решите...
skskanshhd skskanshhd  03.09.2020 17:55
1. Найдите площадь квадрата если его диагональ равна 4. 2. Найдите площадь прямоугольника сторона которой равна 5 а диагональ 13 .3. Найдите площадь прямоугольника если его периметр...
ренатик9 ренатик9  04.09.2020 17:35
Выписать все определения многоугольников и геометрических фигур​...
SuperMaksni4ic SuperMaksni4ic  03.09.2020 18:00
Тікбұрыш үшбұрыш: а)теңбүйірлі ә)тенқабырғалы болцы мүмкін бе?​...
алинкаблн алинкаблн  20.05.2020 14:01
Сырттай жанасқан екі шеңбердің центрлерінің арақашықтығы 24 см.Бірінші шеңбердің радиусы екіншісінен 3 есе артық.Шеңберлердің радиустарын табыңыз....
valwkebe valwkebe  20.05.2020 14:01
угол BAK=угол CAK Довести что треугольник ABK= треугольник ACK...

Популярные вопросы