Площадь правильного шестиугольнику равна 64. найти площадь шестиугольника последовательным соединением середин его сторон?

Данный правильный 6-иугольник  состоит из 6 правильных треугольников со стороной а.       S = 6*[a^2 *(кор3)/4] = 64.

Новый 6-иугольник также будет правильным, но со стороной b, равной апофеме исходного 6-иугольника:

b = a(кор3)/2.

Его площадь:

S1 = 6*[b^2 *(кор3)/4] = (3/4)*6*[a^2 *(кор3)/4] = (3/4)*S = 48.

ответ: 48

Площадь полученного шестиугольника будет меньше площади данного шестиугольника на шесть площадей равных равнобедренных треугольников. У этих треугольников боковые стороны равны ½ стороны данного шестиугольника, а угол между ними равен 120⁰.

SΔ= ½ ab · sin γ

S = ½ · ¼a² · (√3)/2 =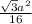  (кв.ед.)

Из формулы площади шестиугольника S=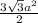 выражаем сторону а:

Подставляя в формулу площади треугольника, находим, что SΔ = 8/3 кв.ед.

6SΔ = 16 кв.ед.

Площадь полученного шестиугольника равна 64-16=48 (кв.ед.)