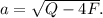Площадь полной поверхности правильной четырехугольной пирамиды равна q ,площадь одной боковой грани равна равна f .выразите сторону основания пирамиды через q и f
Другие вопросы по теме Геометрия
Популярные вопросы
- Log по основанию 1/16 5 корней из 64...
1 - Данные слова абрикос банан груша брусника крыжовник малина все эти слова...
3 - Нужно заранее большое ) брусок скатится с наклонной плоскости длиной...
1 - Лексическое значение слова грибница....
3 - Один из корней уравнения 3х в квадрате - 21х + q= 0 меньше одного на...
2 - Сочинить текст про животное сначала написать что тебя в нём удевляет,...
1 - Этот квадрат разделили на16 маленьких квадратиков.проведи два отрезка...
2 - Назвати компоненти у рівностях 3 умножить 4 =12...
2 - Структурная и электронная формулы молекул n2, o2, f2.почему азот встречается...
1 - Станок- автомат изготовил 348 деталей по 58 деталей в час. сколько деталей...
3
В основании правильной четырёхугольной пирамиды лежит квадрат, а боковые грани это равные треугольники, всего 4 боковых грани.
S(бок.) = 4F.
S(полн.) = S(бок.) + S(осн.);
S(осн.) = S(полн.) - S(бок.) = Q-4F
Площадь основания (квадрата) равна квадрату его стороны (a).
a² = S(осн.) = Q-4F
a = +√(Q-4F) т.к. t > 0.
ответ: