1. Геометрия
  2. Площадь круга вписанного в квадрат

Площадь круга вписанного в квадрат 16 пи сантиметров квадратных. найти сторону квадрата описанного и вписанного кол.

jojo31 jojo31    3   10.06.2019 00:20    4

Ответы
Sashaklapp Sashaklapp  08.07.2020 15:22
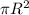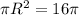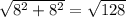\pi R^{2} - площадь круга в целом, \pi R^{2}=16 \pi, сокращаем пи, получаем R^{2}=16; R=4, это был радиус вписанного в квадрат круга, а описанный около квадрата имеет радиус, равный половине диагонали, диагональ по теореме Пифагора, сторона квадрата равна удвоенному радиусу вписанного круга, т.е. 8 см, \sqrt{ 8^{2} + 8^{2} }= \sqrt{128}, а у нас радиус равен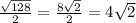\frac{ \sqrt{128} }{2}= \frac{8 \sqrt{2} }{2}=4 \sqrt{2}
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
егормицевич егормицевич  08.02.2021 17:40
Найдите сторону AC треугольника ABC, если AB=10см,BC=12см и Sin B=0,6​...
sergeymo00 sergeymo00  08.02.2021 17:40
Дан треугольник CDE сколько прямых, параллельных стороне CE можно провести через вершину...
Ученик2017gmailcom Ученик2017gmailcom  08.02.2021 17:40
Площадь треугольника АВС равна 4. Точки Д Е серидины сторон АВ и ВС (рис 21.5). Найдите площадь треугольника СДЕ...
KceniaZyikova KceniaZyikova  08.02.2021 17:41
решить) завтра надо исправлять...
rageworker rageworker  08.02.2021 17:41
Bd биссектриса угла b.докажите равенство треугольников abd и cbd​...
Nikaaazhh Nikaaazhh  08.02.2021 17:43
Трапеція Abcd з основами AD i BC та трикутник MEF не дежать в одній площині, точка E - середина відрізка AB, точка F - середина відрізка CD,ME=FE, Кут MEF = 110 грацусів....
doschanov doschanov  24.10.2021 23:34
Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4 : 6....
PROvacaTOR1 PROvacaTOR1  24.10.2021 23:31
Периметр прямокутника дорівнює 72 см. Знайти сторони прямокутника, якщо одна з них дорівнює 2 дм...
liq2354234 liq2354234  24.10.2021 23:28
В четырёхугольнике BDKM угол DKB= углу MBK. Сторона BM лежит в плоскости Альфа. Доказать что DK параллельно альфе...
vadimmikrukov6p07zb1 vadimmikrukov6p07zb1  24.10.2021 23:27
В параллелограмме – середина стороны , точка лежит на стороне так, что : = 1: 2...

Популярные вопросы