Площадь боковой поверхности конуса в два раза больше площади основания. найдите угол между образующей конуса и плоскостью основания
Ответы
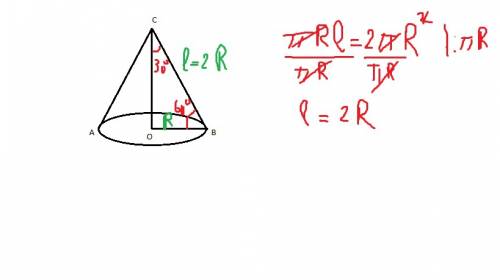
Угол между образующей конуса и плоскостью основания равен углу между образующей и радиусом основания, проведенного к данной образующей. Площадь боковой поверхности конуса: pi*R*l, площадь основания - pi*R^2. Поскольку площадь боковой поверхности в два раза больше площади основания, то pi*R*l = 2*pi*R^2. упрощаем уравнение: l = 2R. Из рисунка CB = 2OB. Из прямоугольного треугольника COB: угол, который лежит против катета, который в два раза меньше гипотенузы, равен 30 градусов. OB - катет, CB - гипотенуза, следовательно, угол BOC = 30 градусов. Искомый угол CBO = 90 - 30 = 60 градусов.
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Yes, it is it a very big village.there...
3 - Перевести,,не через переводчик ты держишь свое слово? да,я всегда держу свое слово...
2 - Вравнобедренном треугольнике skp с основанием sp, из вершины k проведена высота....
3 - Назовите продукты реакции стронция с хлором...
3 - Подобрать проверочные слова.к слову радостный,грустный,грозный,поздний,известный,ужасный,звёздный,...
2 - Раскройте скобки, выбирая правильную форму глагола. 1. they (posted/were posted)...
1 - Решите уравнение (327x-5295)÷57=389...
3 - Может написать 5 предложений про сноуборд на казахском языке) заранее ♡...
2 - Написать православные праздники . какие из них мы отмечаем и дату....
2 - Написать славарные слова на тему огород...
3