1. Геометрия
  2. Площа рівнобічної трапеції,

Площа рівнобічної трапеції, описаної навколо круга, дорівнює S. Знайти бічну сторону трапеції, якщо гострий кут при основі дорівнює 60градусів.

кракодиллох кракодиллох    1   09.08.2022 07:54    1

Ответы
zarinaa2004 zarinaa2004  09.08.2022 07:55

Боковая сторона трапеции равна \sqrt[4]{{\frac{{4{S^2}}}{3}}}

Объяснение:

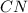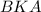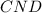Опустим высоты BK и CN на нижнее основание трапеции. Тогда прямоугольные треугольники BKA и CND равны.

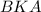Пусть боковая сторона трапеции AB = CD = x.  Из треугольника BKA через метрические соотношения

BK = x\sin 60^\circ = \displaystyle\frac{{\sqrt 3 }}{2}x.

Условием того, что в четырехугольник можно вписать окружность, является равность сумм противоположных сторон. Значит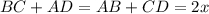 BC + AD = AB + CD = 2x.

По формуле площади трапеции

S = \displaystyle\frac{{AB + CD}}{2} \cdot BK = \displaystyle\frac{{2x}}{2} \cdot \displaystyle\frac{{\sqrt 3 }}{2}x = \displaystyle\frac{{\sqrt 3 }}{2}{x^2},

откуда

{x^2} = \displaystyle\frac{{2S}}{{\sqrt 3 }}; x = \sqrt {\displaystyle\frac{{2S}}{{\sqrt 3 }}} = \sqrt[4]{{\displaystyle\frac{{4{S^2}}}{3}}}.


Площа рівнобічної трапеції, описаної навколо круга, дорівнює S. Знайти бічну сторону трапеції, якщо
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Demo180 Demo180  21.05.2020 21:44
Шар ограничен сферой с центром A радиуса 3 см. Точки B,C и D расположены в так, что AB=25 мм, AC=3 см, AD=0,4 дм. Запишите только верные утверждения....
blvckbubblegum blvckbubblegum  22.05.2020 00:30
Соч геометрия Радиусы 15 см - ге тең шеңбердің , градустық өлшемі 36 -қа тең доғасының ұзындығын Taп 2.Дөңес бесбұрыштың бұрыштары1,3,5,7 , 11 сандарына пропорционал . Дөңес...
HETHEDAM HETHEDAM  22.05.2020 06:00
Дана окружность с центром о. в скольких точках пересекает её...
bika20679 bika20679  22.05.2020 05:37
Найдите площадь трапеции изображённой на клетчатой бумаге с размером клетки 1см х 1см....
Adinay12 Adinay12  22.05.2020 05:41
Длина тени многоэтажного здания равна 6 м, а длина тени вертикально закреплённого колышка равна 1 м. Вычисли высоту здания, если высота колышка равна 1,3 м....
olegyagubov01 olegyagubov01  22.05.2020 22:28
Знайді кути А і С якщо АВ=ВС кут В =42 градуси...
Desa11 Desa11  22.05.2020 22:28
К плоскости проведен перпендикуляр АВ и две наклонные АС и АД. Угол АСВ равен 30°, АС = 16 см, ВД = 6 см. Найти длину наклонной АД. Решение с фото и чертежом ....
Ларкия Ларкия  22.05.2020 22:29
Точка О – центр кола, В =500. Знайдіть градусну міру АОС? А) 960; Б) 480; В) 250; Г) 1000....
yvtcrvt yvtcrvt  10.12.2019 13:15
21 , help! умоляю, ! небольшое, несложное , но нужно ! только, , верно, подробно и понятно. чтобы все было расписано/с объяснением и т.п.​...
sofiazahhа sofiazahhа  10.12.2019 13:16
Отрезки ав и мn пересекаются в точке о и делятся пополам. докажите равенство треугольников аом и nob ​...

Популярные вопросы