Площа рівнобічної трапеції, описаної навколо кола, дорівнює S. Висота трапеції вдвічі менша від бічної сторони. Знайти радіус вписаного кола.
Другие вопросы по теме Геометрия
Популярные вопросы
- Написати міні-твір продовживши речення: Я дивлюсь у вікно, тому...
3 - 2 задания по информатике из темы объекты компьютерной графики...
2 - Найдите сумму, разность, произведение и частное комплексных чисел...
3 - Складзице сказ па схеме [ ], (дзе ...)....
1 - 2. Выполнить рисунок на альбомном листе к стихотворению: Если...
3 - 4) Бутенко и Семенов имеют вместе 26 шаров; Семенов и Лысенко...
3 - Крупнейшая пустыня Северной Америки....
2 - Какие регионы страны могут быть использованы для отдыха и туризма?...
2 - Установите, что из перечисленного относится к компетенции Совета...
1 - До школи привезли 16 ящиків крейди по 6 кг у кожному. У першій...
3
Радиус вписанной окружности равен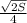
Объяснение:
Проведем в трапеции высоты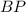 и
и 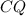 к нижнему основанию.
к нижнему основанию.
Пусть высота трапеции равна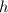 , тогда боковая сторона трапеции по условию равна
, тогда боковая сторона трапеции по условию равна 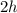 .
.
Условие того, что в четырехугольник можно вписать окружность, — равенство сумм противоположных его сторон.
Таким образом, сумма оснований равна сумме боковых сторон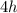 , а средняя линия
, а средняя линия
Площадь трапеции
Так как высота трапеции — расстояние между основаниями — равна диаметру окружности, то радиус вписанной окружности