Перпендикуляр, который проведён из вершины прямоугольника к его диагонали, делит прямой угол в отношении 2 : 1. вычисли острый угол между диагоналями прямоугольника.
Ответы
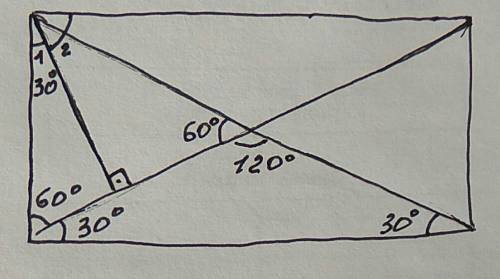
Перпендикуляр, опущенный к диагонали из прямого угла, образует два угла, один из которых составляет 1 часть, а другой - 2 части. В сумме прямой угол составляет 3 части, значит 90:3=30° Это меньший угол. В прямоугольном треугольнике, получившемся при проведении перпендикуляра, находим третий угол между стороной прямоугольника и его диагональю 180-(30+90)=60° Его смежный угол равен 90-60=30° В треугольнике, образованном стороной прямоугольника и его диагоналями, углы при основании равны, т. к. он равнобедренный. Угол при вершине этого треугольника равен 180-(30+30)=120° Находим искомый острый угол между диагоналями прямоугольника 180-120=60°
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Чи може кут між прямими дорівнювати: 1) 1°; 2) 80°; 3) 90°; 4)...
3 - Кути FOК i МОЕ piвні (рис. 75). Чи pівні кути FOM i КОЕ?...
2 - Промінь ВК є бісектрисою кута CBD, ∟ABK = 146° (рис. 76). Знайдіиь...
3 - Промінь ВК є бісектрисою куга CBD, ∟CBD = 56° (рис. 76). Знайдіть...
1 - Знайдіть кут між стрілками годинника, якщо вони показують: 1)...
2 - Кут ABC дорівнює 30°, кут CBD - 80°. Знайдіть кут ABD. Скікьки...
3 - Скільки пар суміжних кутів зображено на рисунку 85? Назвіть ix....
3 - Чи можуть два суміжних кути дорівнювати: 1) 24° i 156°; 2) 63°...
3 - Знайдіть кут, суміжний із кутом: 1) 29°; 2) 84°; 3) 98°; 4) 135°....
3 - Знайдіть суміжні кути, якщо: 1) один iз них у 17 разів більший...
1