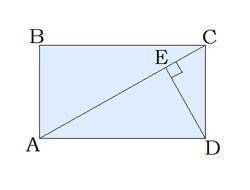
Перпендикуляр, который проведён из вершины прямоугольника к его диагонали, делит прямой угол в отношении 4 : 1. Вычисли острый угол между диагоналями прямоугольника.
Острый угол между диагоналями равен
Другие вопросы по теме Геометрия
Популярные вопросы
- Разложи на множители (t + 12)³ – 0,027...
3 - A. Choose the best word or phrase to fill in the blank. 1. Creams...
3 - Напишите 10 предложений про озеро Алаколь...
3 - Какие княжества были в Южной и юго- западной руси в период раздробленности...
3 - Биология Выполните задание: выберите из приведенных высказываний...
3 - Запишите в виде неравенства и в виде числового промежутка множество...
1 - Составить текст с местоимениями, которые входят в состав фразеологических...
2 - 1Проведите анализ следующих элементов Hg, k, At, по плану: 1)...
1 - Миша загадал двузначное число. какова вероятность того что это...
3 - С какой скоростью распространяется упругая волна, если в некоторой...
2
Видим, что DE делит угол D в отношении 4:1, тогда
∠CDE = 90 : 5 = 18°
∠ACD = 90 - 18 = 72°
проводим вторую диагональ BD, точка пересечения О, треугольник COD равнобедренный (СО=DO), углы при основании равны 72°.
Тогда найдём угол между диагоналями:
180 - 72 * 2 = 180 - 144 = 36°.
ответ: Острый угол между диагоналями равен 36°