Перпендикуляр и наклонные. Угол между прямой и плоскостью
5. Наклонные Перпендикуляр и наклонные. Угол между прямой и плоскостью 5. Наклонные

ответ: АВ = 30 см, DC = 15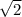 см

Объяснение:

В треугольнике АВД против угла А=30 градусов лежит катет, равный половине гипотенузы.

То есть гипотенуза (наклонная) АВ = 2*DB = 2*15 = 30 см

В прямоугольном треугольнике  DBC оба острых угла равны 45, значит треугольник равнобедренный и ВС = DB = 15 см

Тогда по Пифагору длина наклонной

DC^2 = DB^2 = BC^2 = 15² + 15² = 225+225 = 450

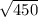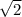Отсюда DC = = 15 см