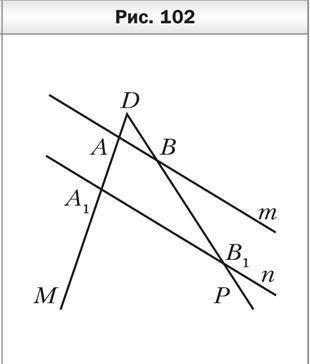
Параллельные прямые m и n пересекают стороны угла МDР (рис. 102). Найдите отрезок АA1, если DА = 8 см,

ВВ1 = 18 см, АА1 = DB. С дано и решение

AA1:8

18:8

Поделить сумму что получилось в AA1:8 на сумму что получилось в 18:8

Для решения этой задачи будем использовать свойство параллельных прямых, которое гласит, что при пересечении прямых параллельных прямых между собой, соответствующие углы равны.

Обратимся к рисунку 102. Заметим, что углы DАD1 и RВ1А1 являются соответственными углами и, следовательно, они равны между собой.

Также заметим, что углы RВ1А1 и МDА являются вертикальными и, следовательно, они равны между собой.

Из условия задачи известно, что DА = 8 см, ВВ1 = 18 см, и АА1 = DB.

Для дальнейшего решения задачи, нам необходимо найти значение отрезка АА1.

Так как углы DАD1 и МDА равны между собой, мы можем записать соответствующие стороны этих углов в пропорции:

DА / МDА = DА1 / D1М

Используем известные значения: DА = 8, DА1 = АА1 и МDА = ВВ1 + DВ

Подставив значения, получим пропорцию:

8 / (ВВ1 + DВ) = АА1 / D1М

Теперь заметим, что углы RВ1А1 и МDР являются соответственными углами и, следовательно, они равны между собой.

Это значит, что стороны АА1 и MD должны быть пропорциональны сторонам ВВ1 и МР.

Таким образом, мы можем записать следующую пропорцию:

АА1 / MD = ВВ1 / МР

Подставив известные значения, получим:

АА1 / (ВВ1 + DВ) = ВВ1 / МР

С нашей первой пропорцией мы можем получить выражение для АА1:

АА1 = D1М * ВВ1 / (ВВ1 + DВ)

Подставим известные значения:

АА1 = (ВВ1 + 8) * ВВ1 / (ВВ1 + 18)

Теперь можем подставить известные значения:

АА1 = (18 + 8) * 18 / (18 + 18)

АА1 = 26 * 18 / 36

АА1 = 13 * 2

АА1 = 26

Итак, длина отрезка АА1 равна 26 см.