Параллельность плоскостей.

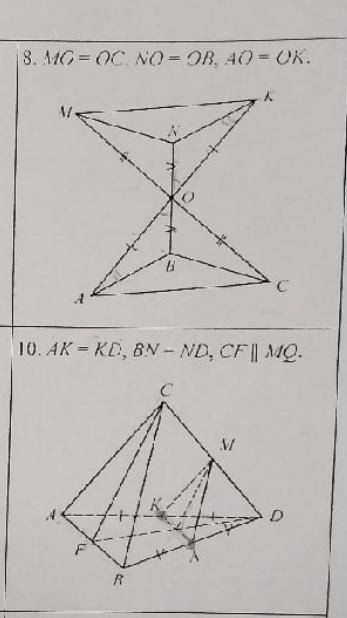
Докажите, что (ABC)||(MNK).

Решите хотя бы одну вас!

Для начала, давайте определим, что такое параллельные плоскости. Плоскости называются параллельными, если они не пересекаются ни в одной точке. Это означает, что все прямые, лежащие в одной из этих плоскостей, не пересекают плоскость, а находятся параллельно другой плоскости.

Теперь посмотрим на данное изображение. Нам нужно доказать, что плоскость ABC параллельна плоскости MNK.
Для этого мы можем использовать два свойства, которые помогут нам найти решение.

1. Если две плоскости пересекают одну и ту же прямую, то они параллельны.
2. Если две плоскости перпендикулярны к одной и той же прямой, то они параллельны (в данном случае это векторы AB и NK).

Давайте решим задачу, используя второе свойство.

1. Сначала определим векторы AB и NK.
Вектор AB = координаты точки B - координаты точки A = (3, 0, 2) - (0, 0, 0) = (3, 0, 2).
Вектор NK = координаты точки K - координаты точки N = (3, 2, 0) - (2, 0, 0) = (1, 2, 0).

2. Затем найдем скалярное произведение векторов AB и NK. Возможные способы вычисления скалярного произведения:
- AB · NK = |AB| * |NK| * cos(θ), где θ - угол между векторами AB и NK.
- AB · NK = (AB_x * NK_x) + (AB_y * NK_y) + (AB_z * NK_z), где AB_x, AB_y и AB_z - координаты вектора AB; NK_x, NK_y и NK_z - координаты вектора NK.

Воспользуемся вторым способом:
AB · NK = (3 * 1) + (0 * 2) + (2 * 0) = 3 + 0 + 0 = 3.

3. Теперь найдем модуль (длину) векторов AB и NK:
|AB| = √((AB_x)^2 + (AB_y)^2 + (AB_z)^2) = √((3)^2 + (0)^2 + (2)^2) = √(9 + 0 + 4) = √13.
|NK| = √((NK_x)^2 + (NK_y)^2 + (NK_z)^2) = √((1)^2 + (2)^2 + (0)^2) = √(1 + 4 + 0) = √5.

4. Подставим значения в формулу для скалярного произведения и вычислим угол между векторами:
3 = √13 * √5 * cos(θ).
Для нахождения косинуса угла θ, разделим обе части уравнения на (√13 * √5):
3 / (√13 * √5) = cos(θ).
Узнаем значение косинуса через тригонометрическую таблицу или калькулятор:
cos(θ) ≈ 0.5095.

5. Обратимся к определению косинуса и найдем значение угла θ:
θ = arccos(cos(θ)).
θ = arccos(0.5095).
Воспользуемся калькулятором, чтобы найти приблизительное значение arccos(0.5095) и получим:
θ ≈ 59.83 градусов.

6. Если угол между векторами AB и NK равен 90 градусам (перпендикулярны), то плоскости ABC и MNK параллельны. Но в нашем случае, угол между векторами равен 59.83 градусам, что означает, что плоскости ABC и MNK не перпендикулярны.

7. Исходя из свойств параллельных плоскостей, мы можем сделать вывод, что плоскости ABC и MNK пересекаются одной и той же прямой (вектором), и поэтому они параллельны.

Таким образом, мы доказали, что плоскость ABC параллельна плоскости MNK.