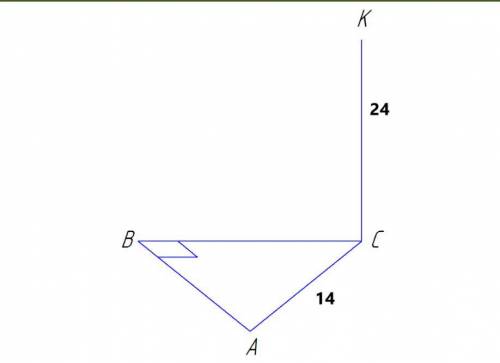
Отрезок КС перпендикулярен АВС. В треугольнике АВС угол В=90 градусов, угол А = 30 градусов, АС= 14. Найдите расстояние от точки K до катета AB,если известно, что CK=24.
Другие вопросы по теме Геометрия
Популярные вопросы
- Во сколько раз данный глобус меньше земли...
2 - Соедини стрелками слова с протвоположным значением fat clean bad long black happy...
1 - Чему равно расстояние от солнца до марса?...
3 - Почему в xiv в. отношение между крестьянами и сеньорами стали более напряжёнными,...
2 - Существует ли треугольник, у которого меньшая сторона составляет 20% от большей,...
2 - Что можно сказать о направлениях векторов импульса и скорости движуйщего тела...
3 - Уровнять реакции: cuch2o5 = cuo + h2o + co2 и cuo + hno3 = cu(oh)2 + h2o...
2 - Выпишите в тетрадь по пять семь стран - крупнейших производителей электроэнергии...
2 - Вчем отличие насекомых от ракообразных и паукообразных...
2 - Синтаксический разбор на казахском пластикалық карталардың басты ерекшелігі-қалтаңызға...
3
Сначала определим длину стороны ВС (гипотенузы треугольника АВС). Так как угол В=90 градусов, мы можем использовать теорему Пифагора:
ВС^2 = АВ^2 + АС^2
ВС^2 = 14^2 + АВ^2
ВС^2 = 196 + АВ^2
Теперь воспользуемся теоремой синусов в треугольнике АВС:
АВ/син(30) = ВС/син(90)
АВ/0.5 = ВС/1
АВ = 0.5 ВС
Подставляем это в наше предыдущее уравнение:
ВС^2 = 196 + (0.5 ВС)^2
ВС^2 = 196 + 0.25 ВС^2
0.75 ВС^2 = 196
ВС^2 = 196 / 0.75
ВС^2 = 261.33
ВС ≈ 16.16 (округляем до двух знаков после запятой)
Теперь, чтобы найти длину отрезка АК, воспользуемся теоремой синусов в треугольнике АКС:
КА/син(90) = КС/син(А)
КА/1 = 24/син(30)
КА = 24 син(30)
КА ≈ 12
Так как нам нужно найти расстояние от точки К до катета АВ, нам нужно вычесть длину отрезка АК из длины катета АВ:
Расстояние = АВ - АК
Расстояние = 16.16 - 12
Расстояние ≈ 4.16
Таким образом, расстояние от точки К до катета АВ составляет примерно 4.16 единицы длины.