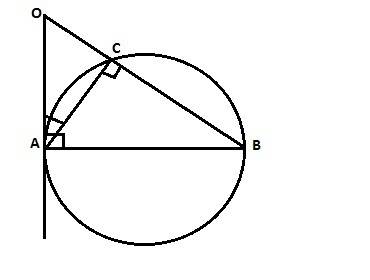
Отрезок ав - диаметр оружности. прямая оа- касательная к окружности, а прямая ов пересекает окружность в точке с. вычислите градусные меры углов треугольника аос , если известно, что дуга вс - дуга ас = 40°

<АСВ=90°,  как вписанный угол, опирающийся на диаметр.Дуга АСВ=180°, так как АВ - диаметр.Сумма градусных мер дуг АС+СВ=180°.Разность дуг BC-АС=40° (дано). Решая систему двух уравнений, имеем:дуга ВС=110°, дуга АС=70°.Угол ОАС между касательной ОА и хордой АС равен половине градусной мерыдуги АС, стягиваемой хордой АС, то есть <OAC=35°. <AОC=180°-35°=55°, (так как сумма острых углов прямоугольного треугольника равна 90°).ответ: углы треугольника АОС: 90°, 55° и 35°.