Отрезок AB = 12 касается окружности радиуса 5 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

8

Объяснение:

Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника  по теореме Пифагора найдём AO:

AO=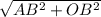==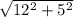13

Найдём AD: AD = AO - OD = 13-5=8

Добрый день! Давайте решим эту задачу пошагово.

1.Дано: У нас есть окружность с центром O и радиусом 5. Мы имеем отрезок AB длиной 12, который касается этой окружности в точке B. Также нам дано, что окружность пересекает отрезок AO в точке D.

2.Решение: Для нахождения AD нам необходимо использовать свойство касательной, перпендикулярного и диаметра окружности.

3.Мы знаем, что AB является касательной к окружности в точке B, поэтому AB и радиус окружности OB, проведенный в точку B, перпендикулярны друг другу.

4.По свойству перпендикуляра, мы можем утверждать, что угол ОВА - прямой угол.

5.Так как угол ОВА - прямой, то треугольник ОВА - прямоугольный.

6.Мы знаем, что в прямоугольном треугольнике гипотенуза в два раза больше катета. В нашем случае ОА - это гипотенуза треугольника ОВА, и ее длина равна AB, то есть 12.

7.Поэтому, для нахождения AD нам нужно разделить гипотенузу ОА пополам.

8.А значит, AD = AB / 2, или AD = 12 / 2 = 6.

Ответ: Длина отрезка AD равна 6.