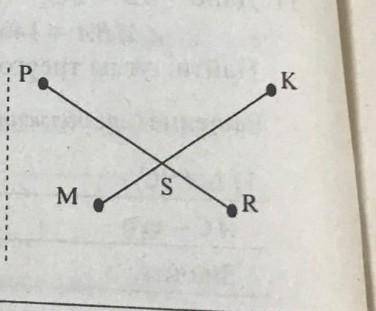
Отрезки MK и PR равны. Дополните рисунок и докажите равенство треугольников KPM и PKR, если известно, что

Чтобы доказать равенство треугольников KPM и PKR, мы можем использовать свойство равенства треугольников, которое гласит: если у двух треугольников равны соответственные стороны и равны соответственные углы между ними, то эти треугольники равны. 1. Возьмем отрезок PK и отложим его от точки P до точки M. Обозначим полученную точку как S. Так как отрезки MK и PR равны, то PS также равен MK. 2. Проведем отрезок SK. 3. Теперь у нас есть два отрезка PK и PR, которые равны, а также отрезки SK и SM, которые также равны, так как это отрезки, полученные разделением отрезка PK на две равные части (по свойству равенства отрезков). 4. Таким образом, у нас есть 3 равных отрезка: PK = PR, SK = SM и MK = PS. 5. Теперь посмотрим на треугольники KPM и PKR. У них соответственные стороны равны: KP = KP (общая сторона), MP = RP (по условию равенства отрезков MK и PR) и MK = PS (получено в предыдущем пункте). 6. Также у треугольников KPM и PKR соответствующие углы равны: угол KPM равен углу PKR (поскольку они вертикальные углы), и угол PKM равен углу PRK (поскольку они углы при равных сторонах MK и PR). 7. Таким образом, у нас есть равные соответственные стороны и равные соответственные углы между треугольниками KPM и PKR. 8. Следовательно, по свойству равенства треугольников, треугольники KPM и PKR равны. Таким образом, мы доказали равенство треугольников KPM и PKR, используя свойство равенства треугольников и известные равенства отрезков MK и PR.