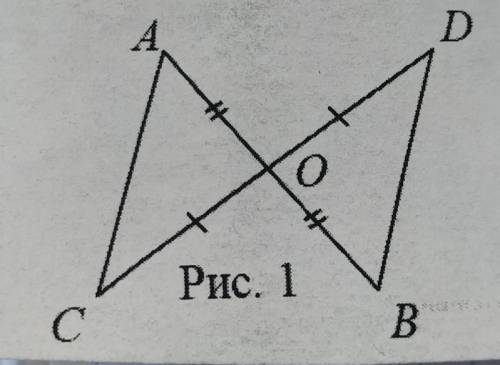
Отрезки AB и CD пересекаются под прямым углом в точке О которая является серединой каждого из них. Найдите утол DBO, если угол ACO равен 30°.
​

Для решения задачи, необходимо разобрать заданный геометрический рисунок и использовать свойства прямых углов и серединных перпендикуляров.

Из условия задачи известно, что точка О является серединой отрезков AB и CD. Это означает, что отрезки AO и OB равны по длине, а также отрезки CO и OD равны по длине.

Рассмотрим треугольник BOC. Известно, что угол ACO равен 30°. Так как точка О является серединой отрезка CD, то угол BOC также равен 30°. Треугольник BOC является прямоугольным, так как угол BOC равен 90° и имеет угол BCO равный 30°. Следовательно, угол BOС также равен 60°.

Теперь рассмотрим треугольник DOB. Так как отрезок AO равен отрезку OB, а угол BOС равен 60°, то треугольник DOB является равнобедренным. Угол DBО является вершинным углом этого равнобедренного треугольника и делится равномерно на две части углами DBО и ОBD. Таким образом, угол DBO равен 30°.

Ответ: Угол DBO равен 30°.