1. Геометрия
  2. Отношение площади основания конуса

Отношение площади основания конуса к площади осевого сечения = пи. найти угол наклона образующей к основанию. нужен полный развёрнутый ответ.

panevin33vladik panevin33vladik    2   16.09.2019 07:10    19

Ответы
Husky333 Husky333  04.08.2020 09:29
S=πR² -- площадь основания конуса
S=1/2*2R*H=RH -- площадь осевого сечения
πR²:RH=π, R:H=1, R=H
tgβ=H/R, tgβ=1, β=45° -- искомый угол
ПОКАЗАТЬ ОТВЕТЫ
ddhfh ddhfh  04.08.2020 09:29

На рисунке в приложении ∆ АСВ - осевое сечение конуса, АВ - диаметр, СМ - высота конуса.

Площадь основания конуса - площадь круга. 

S(кр)=πR²

Площадь осевого сечения - площадь треугольника АСВ. 

S(ACB)=СН•АВ:2=h•R

По условию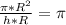 \frac{ \pi * R^{2} }{h*R} = \pi. 

Выразим h из этого уравнения. 

h=πR²:πR ,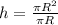 h= \frac{ \pi R^2}{ \pi R} после сокращения получаем h=R

В прямоугольном ∆ АМС катеты АМ=СМ. Этот треугольник равнобедренный.  Острые углы равнобедренного прямоугольного треугольника равны 45°. 

Следовательно, искомый угол 45°


Отношение площади основания конуса к площади осевого сечения = пи. найти угол наклона образующей к о
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
irabirykova18 irabirykova18  14.08.2019 21:40
Две противолежащие стороны четырёхугольника равны 7 см и 13 см. чему равен периметр четырёхугольника, если в него можно вписать окружность? рисунок не прилагается. заранее ....
рустамммм рустамммм  14.08.2019 21:40
При какой температуре начнут образовываться облака в воздухе с абсолютной влажностью 5 г/м(3). рассчитайте высоту, где будет такая температура, если у земной поверхности +18...
Тина551 Тина551  14.08.2019 21:40
При перетині двох паралельних прямою утворилися 8 кутів. різниця між двома з них 90градусів. знайти градусну міру всіх кутів що утворилися....
mspanda22 mspanda22  07.11.2019 19:55
Нарисуйте треугольник abc где bd медиана треугольника abc pabc=65 ab=20 bc=27 ad-? cd?...
УЕД УЕД  07.11.2019 19:55
Как решать(с правильно оформленным решением) такие ? ▲ = знак треугольника дано: ▲rst, rs=st, p=2.5м rt=1.3мнайдите: rs, st....
мангл003 мангл003  07.11.2019 19:57
Второй признак равенства треугольниковвариант 1в четырёхугольнике abcd угол1 = угол2 и угол3 = угол4. докажите, чтоab = cd.ответ: /вна рисунке дана фигура, у которой ad = cf, z bac...
Hacтяя Hacтяя  07.11.2019 19:57
Площина трикутника cdf зі сторонами 3 см, 4 см 5 см паралельна площині b. світло що виходить з точки s, відкидає на площину b тінь c1d1f1 вид трикутника cdf. відомо щоsc: sc1 = 1:...
xandar815 xandar815  07.11.2019 19:58
На рисунке 93 дуга ab = 64 °, дуга bc = 92 °. найдите угол ab....
keshatroy86e7 keshatroy86e7  07.11.2019 19:59
Две стороны треугольника равны 9см и 7см, а угол , противолежащий большей из них равен 60 градусов решите треугольник...
hhjufjifklkl hhjufjifklkl  31.08.2019 12:50
26. биссектриса угла треугольника пересекает сторону под углом 850 и биссектрису одного из углов под углом в 540. найти величины углов треугольника. 27.в треугольнике авс с=900, cd...

Популярные вопросы