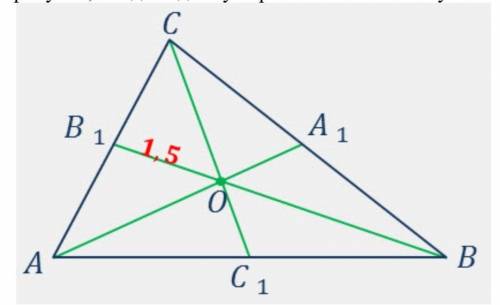
От Точка O - точка пересечения медиан АА1, BB1, СС1. Пользуясь данными рисунка, найдите длину отрезка BO. В ответе укажите только число.
Другие вопросы по теме Геометрия
Популярные вопросы
- 763. 1. Используя данные таблиц 30—31, помещенных на страницах 23—24, округлите...
3 - Перепишите. Слова в скобках поставьте в нужной форме. 1. (Моя подруга) исполнилось...
2 - рассчитайте с какой силой атмосферный атмосферное давление давит на площадь размером...
1 - In the given и тд.( все на фото)...
1 - ма сбора и переработки мусора Вычисли СТОЛБИКОМ...
3 - Найти эквивалентное сопротивлление на контактах X1 и X2 ответ в омах...
1 - Как смотрит дина на русского пленика? Таблица до и после...
3 - ЖАЗЫЛЫМ 7 -тапсырма. Қажетті сөздерді жаз. Қажетті сөздер: жап-жарық, шашып тастаған,...
3 - ПЛАН ВЫСТУПЛЕНИЯ НА ТЕМУ В ЖИЗНИ ВСЕГДА ЕСТЬ МЕСТО ПОДВИГУ (хотя бы 10 пунктов),...
1 - определить вид придаточных) Если вы начали говорить, то лучше договаривать всё...
1
Медианы являются отрезками, соединяющими вершину треугольника с серединой противоположной стороны. Точка пересечения медиан называется центроидом и обозначается буквой O.
Заметим, что медианы разбиваются точкой O на отрезки, пропорциональные длинам оставшихся частей медиан, то есть:
AO:OA1 = BO:OB1 = CO:OC1
Поскольку точка O является точкой пересечения всех медиан, то длина отрезка AO равна длине отрезка OA1, длина отрезка BO равна длине отрезка OB1 и длина отрезка CO равна длине отрезка OC1.
Рассмотрим только отрезок BO, поскольку его длину и ищем. Положим длину отрезка BO равной х.
Тогда согласно пропорциям:
AO:OA1 = BO:OB1 = CO:OC1
мы можем записать:
AO:AO + OA1 = BO:BO + OB1
Подставим известные значения:
AO:AO + 3x = x:x + x + 2
Упростим выражение:
AO:AO + 3x = x:2x + 2
Заметим, что AO равно половине длины медианы, то есть:
AO = AO + OA1 / 2
Подставим это значение в уравнение:
AO + OA1 / 2:AO + OA1 = x:2x + 2
Умножим обе стороны уравнения на (AO + OA1):
(AO + OA1) * (AO + OA1 / 2) = (AO + OA1) * (x / (2x + 2))
Раскроем скобки:
(AO^2) + (AO * OA1 / 2) + (OA1^2 / 4) = (x * AO + x * OA1) / (2x + 2)
Домножим обе стороны уравнения на 4(2x + 2), чтобы избавиться от знаменателя:
4(AO^2) + 2(AO * OA1) + (OA1^2) = 4(x * AO) + 4(x * OA1)
Раскроем скобки:
4(AO^2) + 2(AO * OA1) + (OA1^2) = 4x * AO + 4x * OA1
Сократим подобные слагаемые:
4(AO^2) - 4x * AO + 2(AO * OA1) - 4x * OA1 + (OA1^2) = 0
Объединим подобные слагаемые:
4(AO^2 - x * AO + AO * OA1 - x * OA1 + (OA1^2)) = 0
Упростим выражение:
4(AO^2 + AO * OA1 - x * (AO + OA1) + (OA1^2)) = 0
Разделим оба выражения на 4, чтобы избавиться от множителя перед скобками:
AO^2 + AO * OA1 - x * (AO + OA1) + (OA1^2) = 0
Заметим, что AO равняется половине стороны треугольника (AO = AB / 2) и OA1 также равно половине стороны треугольника (OA1 = BC / 2). Таким образом, мы можем заменить AO и OA1 на известные значения:
(AB / 2)^2 + (AB / 2) * (BC / 2) - x * ((AB / 2) + (BC / 2)) + (BC / 2)^2 = 0
Упростим выражение:
(AB^2 / 4) + (AB * BC / 8) - x * ((AB + BC) / 4) + (BC^2 / 4) = 0
Умножим уравнение на 8, чтобы избавиться от знаменателя:
2AB^2 + AB * BC - 2x * (AB + BC) + 2BC^2 = 0
Теперь у нас есть квадратное уравнение, которое можно решить для x.
AB^2 + AB * BC - 2x * (AB + BC) + BC^2 = 0
Решим уравнение:
AB^2 + AB * BC - 2x * (AB + BC) + BC^2 = 0
Раскроем скобки:
AB^2 + AB * BC - 2x * AB - 2x * BC + BC^2 = 0
Упростим выражение:
(AB^2 + BC^2) + (AB * BC - 2x * AB - 2x * BC) = 0
Поменяем местами слагаемые:
(AB^2 + BC^2) - (2x * AB + 2x * BC - AB * BC) = 0
Объединим подобные слагаемые:
(AB^2 + BC^2) - (2x * (AB + BC) - AB * BC) = 0
Воспользуемся формулой для разности квадратов, чтобы преобразовать уравнение:
(AB - BC)^2 - (2x - AB * BC)(AB + BC) = 0
Положим (AB - BC)^2 = a и (2x - AB * BC)(AB + BC) = b, чтобы сократить запись:
a - b = 0
Подставим значения a и b:
(AB - BC)^2 - (2x - AB * BC)(AB + BC) = 0
Произведем раскрытие скобок:
(AB^2 - 2AB * BC + BC^2) - (2x * AB + 2x * BC - AB * BC - BC^2) = 0
Упростим выражение:
AB^2 - 2AB * BC + BC^2 - 2x * AB - 2x * BC + AB * BC + BC^2 = 0
Объединим подобные слагаемые:
AB^2 - 2AB * BC + AB * BC - 2x * AB - 2x * BC + BC^2 + BC^2 = 0
Распишем слагаемые:
AB^2 - 2AB * BC + AB * BC - 2x * AB - 2x * BC + BC^2 + BC^2 = 0
Сгруппируем слагаемые:
(AB^2 - 2AB * BC + AB * BC) - (2x * AB + 2x * BC) + (BC^2 + BC^2) = 0
Рассмотрим проведенные выше действия. В итоге мы получили квадратное уравнение вида:
a - b = 0
Теперь, чтобы найти длину отрезка BO, мы должны решить это квадратное уравнение.
Подставим известные значения AB=12, BC=16:
(12^2 - 2 * 12 * 16 + 12 * 16) - (2x * 12 + 2x * 16) + (16^2 + 16^2) = 0
Выполним простые арифметические операции:
(144 - 384 + 192) - (24x + 32x) + (256 + 256) = 0
(144 - 384 + 192) - (56x) + (256 + 256) = 0
(-48) - (56x) + (512) = 0
Перенесем все числа на одну сторону уравнения и упростим:
-56x - 48 + 512 = 0
-56x + 464 = 0
-56x = -464
x = -464 / -56
x = 8.3
Таким образом, длина отрезка BO равна примерно 8.3 (число указывается без указания десятичных знаков, округленное до ближайшего целого числа).