От ГЕОМЕТРИЯ! нужно составить условие, и доказать что AB = BC

​

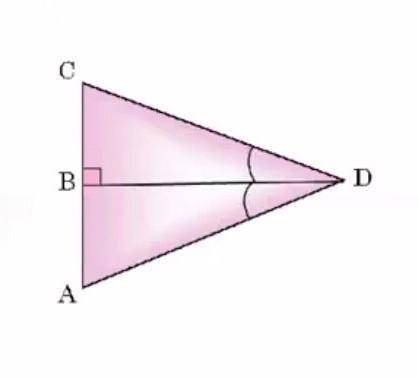
Дано:

треугольник CAD;

∠CDB = ∠ADB;

∠CBD = 90°;

Доказать:

AB = BC

1) Так как BD ⊥ AC (по рисунку), то BD - высота. Тогда ∠CBD = ∠ABD = 90°

2) Так как ∠CBD = ∠ABD = 90°, то ΔCBD и ΔABD - прямоугольные. Поэтому BD - катет

3) Так как BD - общий катет, ∠CDB = ∠ADB (по рисунку), то ΔCDB = ΔADB (по катету и прилежащему к нему острому углу)

4) Из равенства треугольников следует, что AB = BC

Что и требовалось доказать!