Осталось немного во знатоков мне.
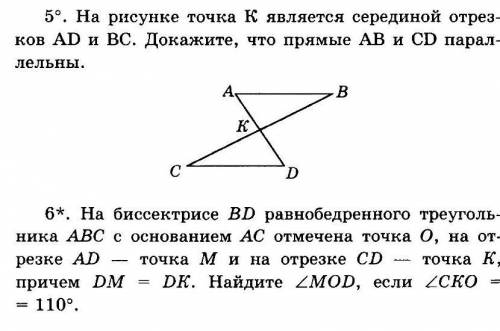
Номер 5 и 6 нужно сделать)​

AD пересекает BC = K;

AK = KD;

BK = KC;

AB || CD.

AK = KD (по условию); |

BK = KC (по условию); |=> △AKB = △CKD (по I признаку).

∠АКВ = ∠CKD, они вертикальные |

Из этого следует, что накрест лежащие ∠KAB = ∠KDC => AB || CD.

△ABC - равнобедренный;

BD - биссектриса;

∠CKO = 110˚;

DM = DK;

O ∈ BD;

M ∈ AD;

K ∈ CD.

∠MOD = ?˚.

∠CKO + ∠OKD = 180˚, т.к. они смежные => ∠OKD = 180˚ - 110˚ = 70˚.

Биссектриса, проведённая к основанию равнобедренного треугольника, является и медианой и высотой.

=> ∠BDC = ∠BDA = 90˚ => △ODK и △ODM - прямоугольные.

Сумма острых углов в прямоугольном треугольнике равна 90°.

=> ∠DOK = 180˚ - (90˚ + 70˚) = 180˚ - 160˚ = 20˚.

MD = DK (по условию); OD - общий катет => △ODM = △ODK.

=> ∠DOK = ∠MOD = 20˚.