Основой пирамиды служит треугольник, площадь которого ровна 9 корней из 5 см2. одна из боковых граней пирамиды перпендикулярный плоскости основы и ровный корень из 5 см. найдите объём пирамиды.
Другие вопросы по теме Геометрия
Популярные вопросы
- Хел При якій силі струму проводився електроліз, якщо за 20 хв на катоді виділилося...
2 - Какой частью речи обычно выражается обращение...
2 - решить задание про past simple...
2 - З якою швидкістю повинен рухатися електрон, щоб його кінетична енергіядорівнювала...
3 - Човен власна швидкисть якого 18 км/ год пройшов 40 км за течією 16 км проти течії,...
3 - Бір мемлекеті таңдап оған жоспар бойынша сипаттама бер Жоспар: 1. Елдің атауы;...
2 - Является ли числоваяпоследовательность 2; 8; 32;128; ... геометрическойпрогрессией?...
2 - даю. Спишите, объясните постановку знаков препинания 1.Чьи-то шаги, правда ещё...
1 - Тәуке ханның мемлекетті нығайтудағы рөлі...
2 - Закон движения точки по прямой задаётся формулой s(t)=6t+2, где t — время (в секундах),...
2
Для нахождения объёма пирамиды необходимо знать площадь фиугры в основании и высоту пирамиды:
Нам дана площадь основания (9 корней из 5).
Так как одна из боковых граней перпендикулярна плоскости основания, то она является высотой пирамиды (по свойствам ортогональной проекции).
Значит объём пирамиды:
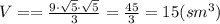
ответ: 15 см3.