Основи рівнобічної трапеції дорівнюють 10см та 18см. Знайдiть видризок, на якi висота, проведена з вершини тупого кута, ділить велику основу.
Другие вопросы по теме Геометрия
Популярные вопросы
- Составитт 20 слов по правилам 5 - 6класса бабайцева...
3 - Reading read the title and the introduction.what is the text about...
2 - Как связана скорость волны с длиной волны и периодом колебаний? с длиной...
2 - Нужно выписать все предложения с причастиями из л.н.толстого бедные лыди...
3 - дан треугольник fkt. постройте векторы, равные сумме разности векторов:...
1 - Наблюдение за кошкой этапы наблюдения...
1 - Стороны треугольника равняются 8 см, 10 см и 14 см. найдите сумму средних...
2 - Ть скласти діалог, використовуючи вигуки, на тему як народжуються народнопісенні...
3 - Почему две прямые, перпендикулярные к третьей прямой, параллельны?...
3 - 3.рассмотрите картинки. запишите вопросы, которые у вас возникли по ходуизучения...
2
Отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание равны 4 см и 14 см.
Объяснение:
Основы равнобедренной трапеции равны 10 см и 18 см. Найдите отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание.
Дано: ABCD - равнобедренная трапеция.
ВС = 10 см; AD = 18 см.
ВЕ - высота.
Найти: BC и AD.
Высота, опущенная из вершины тупого угла равнобедренной трапеции на большее основание, делит его на части, меньшая из которых равна полуразности оснований, а большая - полусумме оснований.⇒ АЕ = (AD - BC) : 2 = (18 - 10) : 2 = 4 (см)
ED = (AD + BC) : 2 = (18 + 10) : 2 = 14 (см)
Докажем это свойство.
Пусть ВС = а, а AD = b.
Опустим еще один перпендикуляр CH на AD.
Рассмотрим ЕВСН.
ВС || EH (условие)
ВЕ ⊥ AD; CH ⊥ AD.
Если две прямые перпендикулярны третьей, то они параллельны между собой.⇒ BE || CH.
ЕВСН - параллелограмм (по определению)
Все углы прямые.
⇒ ЕВСН - прямоугольник.
В прямоугольнике противоположные стороны равны.⇒ ВС = ЕН = а
Рассмотрим ΔАВЕ и ΔHCD - прямоугольные.
АВ = CD (ABCD - равнобедренная трапеция)
Углы при основании равнобедренной трапеции равны.∠A = ∠D
ΔАВЕ = ΔHCD (по гипотенузе и острому углу)
⇒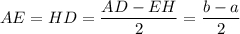
ED = HD + EH
Отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание равны 4 см и 14 см.
#SPJ1