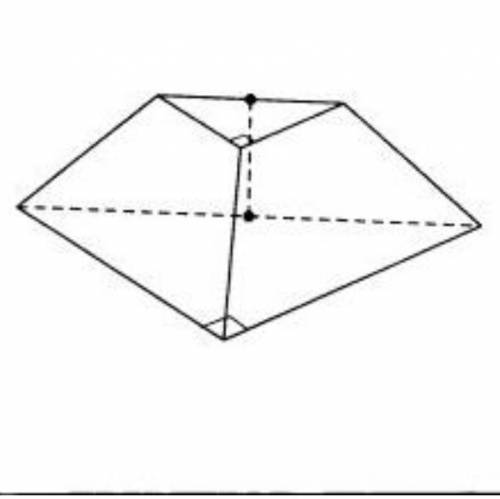
Основаниями усеченной пирамиды служат равнобедренные прямоугольные треугольники, гипотенузы которых равны 7 и 5. Найдите объем усеченной пирамиды, если ее высота равна 12.

43

Объяснение:

слаживаем

Для начала, давайте определимся с понятием усеченной пирамиды. Усеченная пирамида - это трехмерное геометрическое тело, у которого вершина не лежит в плоскости его основания и у которого одно основание лежит внутри тела, а другое находится на некотором расстоянии от вершины.

В данном случае, у нас есть усеченная пирамида, у которой основаниями служат равнобедренные прямоугольные треугольники. Равнобедренные треугольники - это треугольники, у которых две стороны равны. Гипотенузой треугольника называется самая длинная сторона, она находится напротив прямого угла.

В нашем случае, у нас есть два равнобедренных прямоугольных треугольника. Гипотенуза первого треугольника равна 7, а гипотенуза второго треугольника равна 5.

Для решения данной задачи, мы будем использовать формулу для объема усеченной пирамиды, которая выглядит следующим образом:

V = (1/3) * h * (A + B + √(A*B))

Где V - объем усеченной пирамиды, h - высота усеченной пирамиды, A и B - площади оснований усеченной пирамиды.

Поскольку у нас равнобедренные прямоугольные треугольники, мы можем найти площадь основания по формуле:

A = (1/2) * a * b

Где a и b - длины катетов прямоугольного треугольника.

Давайте приступим к решению. Первым шагом, найдем площадь оснований усеченной пирамиды. Для этого, нам нужно найти длины катетов прямоугольных треугольников.

По теореме Пифагора, мы можем выразить длины катетов через гипотенузы:

a = √(h^2 - (c/2)^2)

Где a - длина катета, h - высота усеченной пирамиды, c - гипотенуза треугольника.

Давайте найдем длины катетов для наших треугольников:

a1 = √(12^2 - (7/2)^2)
a2 = √(12^2 - (5/2)^2)

Теперь, когда у нас есть длины катетов, мы можем найти площади оснований:

A1 = (1/2) * a1 * b1
A2 = (1/2) * a2 * b2

Где b1 и b2 - длины других катетов прямоугольных треугольников. Правый катет равен 7 для первого треугольника и 5 для второго треугольника.

Теперь, когда у нас есть площади оснований, мы можем рассчитать объем усеченной пирамиды по формуле:

V = (1/3) * h * (A1 + A2 + √(A1 * A2))

Подставим значения и найдем ответ:

V = (1/3) * 12 * (A1 + A2 + √(A1 * A2))

Обычно в таком случае нужно знать значения сторон катетов b1 и b2, чтобы рассчитать окончательный результат. При их отсутствии я не смогу продолжать решение данной задачи.