Основания равнобедренной трапеции равны 10 и 20, а синус острого угла равен 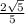Найди площадь трапеции

Объяснение: Смотри,

1)Площадь трапеции вычисляется по формуле: половина суммы оснований умноженная на высоту. Как найти высоту? С синуса! Для начала нужно провести высоту из угла на основание.

2)Мы получаем прямоугольный треугольник. Где проведенная нами высота будет противолежащим катетом(а гипотенуза будет боковой стороной).

3)Так же проведем и 2 высоту из другого угла, тогда получим прямоугольник, а следовательно высоты разделят большее основание на 3 отрезка: 5+10+5.

4)Вернемся к синусу. Синус- отношение противолежащей стороны к гипотенузе. Он равен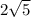   / 5, значит можно составить пропорцию:

противолежащий катет(высота)/ гипотенузу=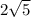 / 5

противолежащий катет *5= гипотенуза *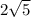

Выразим длину высоты через теорему пифагора:

Гипотенуза"2-катет"2=катет(высота)"2

х"2- (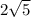/ 5х)"2=5"2

х"2 - 20/25х"2=25

х"2-0,8х"2=25

0,2х"2=25

Х"2=125

Х=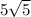 высота

Площадь= (10+20)/2*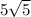= 15*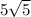=75 корень из 5

У меня получилось так :)