1. Геометрия
  2. Основанием прямой треугольной

Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 13 см и катетом 5 см высота призмы равна радиусу окружности вписанного в основание

Simps0n Simps0n    2   31.07.2019 02:30    10

Ответы
Sweet572 Sweet572  03.10.2020 18:11

Рассмотрим прямоугольный треугольник ABC в нём AC=13 см и AB = 5 см. По теореме Пифагора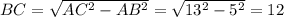 BC=\sqrt{AC^2-AB^2} =\sqrt{13^2-5^2}=12 см



Радиус вписанной окружности в основание равно: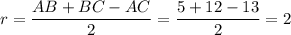 r=\dfrac{AB+BC-AC}{2}=\dfrac{5+12-13}{2}=2 см.

Из условия, высота призмы равна радиусу вписанной окружности в основание, то есть: AA_1=r=2 см



Объём призмы: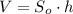 V=S_o\cdot h, где So - площадь основания, h - высота призмы.


Площадь основания: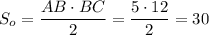 S_o=\dfrac{AB\cdot BC}{2}=\dfrac{5\cdot 12}{2}=30 см²



Окончательно получим: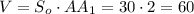 V=S_o\cdot AA_1=30\cdot2=60 см³



ответ: 60 см³.


Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 13 см и катетом
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Regisha1981 Regisha1981  09.03.2019 13:00
Катет прямоугольного треугольника равен 12 см,а его проекция на гипотенузу равна 8 см.найти площадь треугольника....
ksun2003 ksun2003  09.03.2019 13:00
(1+ctg квадратальфа)*sin квадратальфа-cos квадратальфа....
Largo2000 Largo2000  09.03.2019 13:00
Востром треугольнике mnp биссектриса угла m пересекает высоту nk в точке o причём ok =9 см найти расстояние от точки o до прямой mn...
monyamirzoeva monyamirzoeva  09.03.2019 13:00
Диагональ куба равна 6 корней из 3 см. найдите площадь грани куба....
ehidna666 ehidna666  09.03.2019 13:00
Найти объем шара, вписанного в куб. площадь поверхности куба равна 72 см в квадрате...
степан169 степан169  09.03.2019 13:00
Хорда,перпендикулярна диаметру,делит его на отрезки,разность которы равна 7см.найдите радиус окружности,если длина хорды равна 24см...
МОЗГ1987 МОЗГ1987  09.03.2019 13:00
Найдите площадь поверхности правильной четырехугольной пирамиды , стороны основания которой равны 6 и высота 4 см...
solodovnikovay124 solodovnikovay124  09.03.2019 13:00
Втреугольнике авс угол в =48(град), а внешний угол при вершине а =100(град) найдите угол вса...
Vika7791532 Vika7791532  12.04.2020 17:17
В пря­мо­уголь­ном тре­уголь­ни­ке с ост­рым углом в 30° боль­ший катет равен равен 18 см. На какие от­рез­ки делит этот катет бис­сек­три­са боль­ше­го остро­го угла тре­уголь­ни­ка?​...
valera555132 valera555132  12.04.2020 17:17
В пятиугольнике АВСДЕ АВ=ВС=СД=ДЕ . Угол В=90, угол С=36, Угол Д=270. Чему равен угол Е?...

Популярные вопросы