Основанием прямой призмы является прямоугольник со сторонами 6 см и 8 см, а диагональ призмы образует с плоскостью основания угол 45 градусов. найдите площадь боковой поверхности призмы. ​

280 см²

Объяснение:

Найдём диагональ d прямоугольника-основания призмы как гипотенузу в прямоугольном треугольнике, образованном сторонами основания и его диагональю. Она является проекцией диагонали призмы на основание, а также катетом в прямоугольном треугольнике, образованном катетом - ребром призмы (равным высоте призмы) , катетом - диагональю основания и гипотенузой - диагональю призмы.

d=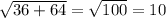

Прямоугольный треугольник, в котором есть внутренний угол 45°, является равнобедренным, поэтому высота призмы равна диагонали основания, как два катета в равнобедренном прямоугольном треугольнике.

Площадь боковой поверхности узнаем, вычислив периметр основания и умножив его на высоту призмы.

Sбок.=P·d=(6+8)·2·10=280 см²