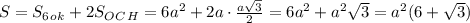Основанием прямого параллелепипеда abcda1b1c1d1 является ромб abcd, сторона которого равна а и угол равен 60о. плоскостьad1c1 составляет с плоскостью основания угол 60о. найдите: а) высоту ромба; б) высоту параллелепипеда; в) площадь боковой поверхности параллелепипеда; г) площадьповерхности параллелепипеда.

Линия пересечения плоскости  AD₁C₁ и плоскости основания есть ребро параллелепипеда АВ.

Угол между плоскостью AD₁C₁ и плоскостью основания есть угол между плоскостью  AD₁C₁ перпендикуляром к АВ, то есть высотой ромба. На рисунке обозначена как ВН.

ΔСВН - прямоугольный, с прямым углом Н, по условию острый угол ромба-основания равен 60⁰, отсюда, зная sin60⁰ находим высоту ромба ВН:

а)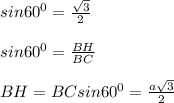 

Можно было вычислить и так, как мы находили АН во вчерашнем задании, через т. Пифагора, зная, что СН=а/2, как катет, лежащий против угла в 30⁰, но сегодня решаем так, чтобы показать разные пути решения.

 б) Высоту параллелепипеда HH₁находим из прямоугольного ΔВН₁Н в котором угол Н прямой, угол В=60⁰, и зная значение tg60⁰:

в) Найти площадь боковой поверхности - самая простая часть этого задания:

, где  и  - периметр основания и высота пераллелепипеда соответственно.

г)