Основанием пирамиды является прямоугольный треугольник с катетами 6 см и 8 см. Все боковые грани с плоскостью основания образуют углы 60° .
Вычисли высоту боковой грани пирамиды.
С РИСУНКОМ
Другие вопросы по теме Геометрия
Популярные вопросы
- Одну из сторон квадрата увеличели на 4 дм а другую уменьшели на 6 дм в результате...
1 - 10 предложений про осень сложные 5 класс...
1 - 100 граммах раствора содержится 1 % соли, затем раствор подвергся испарению...
2 - Фонетический разбор слова нетрудная . )...
2 - Вырази: 9м=скока см 30см=скока дм 184дм=скокам и дм 3ч=скока мин 95с=скока=м...
1 - Укажите ряд в котором все слова однокоренные 1)вода водитель водный 2) лес...
1 - Что обозначают в р.яз цифры 1 2 3 4 5 над словамивведите свой вопрос сюда...
3 - Все о писателе- иванов иванович дмитриев...
2 - Выпишите слово из предложений без окончаний. и слышится далеко крик старого...
3 - Какие корни у слов: чудесный, интересный, неизвестный, прекрасный, участник,...
1
SM = 4 cм
Объяснение:
найдем гипотенузу основания по теореме Пифагора
АВ=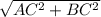 =10
=10
SO высота пирамиды, а OK,OM,ON - серединные перпендикуляры и радиусы вписанной окружности, равные между собой.
Чтобы найти радиус, воспользуемся формулой площади S=pr и
S=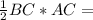 0,5*6*8=24 см^2 Тогда r=S/p, где р- полупериметр =(6+8+10)/2=12, r=24:12=2 см
0,5*6*8=24 см^2 Тогда r=S/p, где р- полупериметр =(6+8+10)/2=12, r=24:12=2 см
Треугольник SOM прямоугольный с углом 60 и 30 градусов, при вершине угол 30 градусов, катет напротив этого угла равен половине гипотенузы, значит гипотенуза (высота боковой грани) SM = 2r=4 cм