Основанием четырехугольной пирамиды является ромб с острым углом 30, а все боковые грани пирамиды наклонены к основанию под углом 60...

Другие вопросы по теме Геометрия
Популярные вопросы
- Фізика,іть будь ласка треба уявити,що морозного дня я прийшла на ковзанку....
1 - Чому сало і загалом свинина вважаються одним з основних украінських продуктів...
3 - На острове было 48 бакланов а деревьях их и 24 хлебный кофейных деревьев в...
1 - 2-метилпентанол-3 по рациональной номенклатуре...
1 - Напишите поздравление другу на казахском, без переводчика и не копируйте с...
2 - Шесть одинаковвых по длительности сеансов радиосвязи продолжались 1 ч 12 мин....
3 - Найдите наибольшее общий делитель и наименьший общее краткое чисел 792 и 1188...
2 - Переведите предложения : асқазан ішілген тамақтан 4 сағат шамасында босайды....
1 - Глаголы с времени с корнем гар и с приставками с-,вы-,до-,на-,за-,раз-,про-,при-,пере-,об-....
1 - Що таке молюски ? які види молюсків є ?...
3
Объяснение:
Дано: KABCD - четырехугольная пирамида, ABCD - ромб, ∠ABC = 30°,
∠(KAB, ABC) = 60°, KO ⊥ ABC,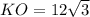 , AC ∩ BD = O
, AC ∩ BD = O
Найти: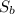 - ?
- ?
Решение: Из точки K проведем перпендикуляр на сторону AB в точку T, то есть KT ⊥ AB по построению. Соединим точки O и T, которые лежат в одной плоскости ABC, то есть прямая OT лежит в плоскости ABC по аксиоме стереометрии. Так как по условию KO ⊥ ABC, то по определению перпендикулярности прямой к плоскости KO перпендикулярно любой прямой лежащей в плоскости ABC, так как OT ⊂ ABC, то KO ⊥ OT. Треугольник ΔKOT - прямоугольный, так как KO ⊥ OT, тогда отрезок OT - проекция KT на плоскость ABC. По теореме о трех перпендикулярах OT ⊥ AB, так как KO ⊥ OT, KT ⊥ AB - по построению и отрезок OT - проекция KT на плоскость ABC из прямоугольного треугольника ΔKOT. Так как OT ⊥ AB по теореме о трех перпендикулярах и KT ⊥ AB - по построению, то угол ∠KTO - линейный угол двухгранного угла между плоскостями KAB и ABC, то есть угол ∠KTO = ∠(KAB, ABC) = 60°. Рассмотрим прямоугольный треугольник ΔKOT: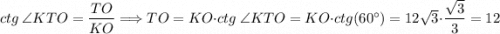 .
.
Так как по условию AC ∩ BD = O, то точка пересечения диагоналей - центр ромба и так как TO ⊥ AB, то отрезок OT - радиус окружности вписанной в ромб. По формуле площади ромба:
Так как по условию все двухгранные углы равны, то по теореме: