Основание равнобедренной трапеции равно 10см,
средняя линия 16см, а меньшая диагональ равна
34см. Найти синус, косинус и тангенс острого угла
трапеции, периметр и высоту трапеции.

ответ: cosД=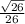;   sinД=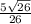;  tgД =5

Р=93,18см, h=30см.

Дано: АВСД- трапеция, АВ=СД, ВС=10см, АС=34см, КМ-средняя линия, КМ=16см.

Найти: cosД-? sinД-?  tgД-?  P-? h-?

Решение: В равнобедренной трапеции углы при основании равны: ∠А=∠Д.

Так как КМ-средняя линия, то КМ=(АД+ВС)/2 →АД=2КМ-ВС,

АД=2*16-10=22(см).

Опустим из ∠С  прямую СС1⊥АД и из ∠В ВВ1⊥АД, СС1=ВВ1= h , ВВ1=ВС,

АВ1=С1Д- так трапеция равнобедренная и  прямоугольные треугольники ΔАВВ1=ΔДСС1. Отсюда С1Д=(АД-ВС)/2=12/2=6(см).

Рассмотрим ΔАВВ1. ∠С1=90°, АС1=АВ1+В1С1=16+10=16(см), АС=34см.

По теореме Пифагора

h²=АС²-АС1²=34²-16²=(34-16)(34+16)= 18*50=900(см²), h= √900=30(см).

Рассмотрим ΔДСС1, ∠С1=90°, С1Д=6см, СС1=30см.

По теореме Пифагора СД²=h²+С1Д=30²+6²=936(см²),

СД=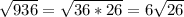(см) или СД=√936≈30,59(см)

Р= АВ+ВС+СД+АД=ВС+АД+2*СД=10+22+2*30,59≈93,18(см)

Косинус угла равен отношению прилежащего катета к гипотенузе

cosД=С1Д/СД=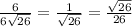

Синус угла равен отношению противоположного катета к гипотенузе

sinД=СС1/СД=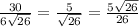

 tgД=30/6=5