Основание прямой призмы-прямоугольный треугольник с катетами 6 и 8 см объем 240. найти площадь полной поверхности

Question

Геометрия: Основание прямой призмы-прямоугольный треугольник с катетами 6 и 8 см объем 240. найти площадь полной поверхности призмы

koteika282 · Answer

Площадь основания (как прямоугольного треугольника) равна половине произведения катетов

S_o=0.5ab=0.5*6*8=24 кв.см

По теореме Пифагора гипотенуза равна

$c=\sqrt{a^2+b^2}=\sqrt{6^2+8^2}=10$ см

Высота призмы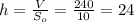 $h=\frac{V}{S_o}=\frac{240}{10}=24$ см

Площадь боковой поверхности призмы

S_b=a*h+b*h+c*h=(a+b+c)*h=(6+8+10)*10=240 кв.см

Площадь полной поверхности

S=S_b+2S_o=240+2*24=288 кв.см

Основание прямой призмы-прямоугольный треугольник с катетами 6 и 8 см объем 240. найти площадь полной поверхности призмы