Основание пирамиды - ромб с большей диагональю d и острым углом альфа. все двугранные углы при основании пирамиды равны бета. найдите площадь боковой поверхности пирамиды.

Ответы

AgataKlemen03 16.08.2020 23:06

Пусть AC - большая диагональ ромба; AC = d и острый угол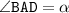 $\tt \angle BAD=\alpha$ . Диагонали ромба являются биссектрисами его углов, пересекаются под прямым углом и в точке пересечения делятся пополам.

$\tt AO=OC=\dfrac{AC}{2}=\dfrac{d}{2};~~~\angle BAO=\angle OAD=\dfrac{\alpha}{2}$

Из прямоугольного треугольника AOD: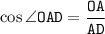 $\tt \cos \angle OAD=\dfrac{OA}{AD}$ отсюда выразим AD: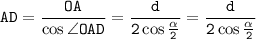 $\tt AD=\dfrac{OA}{\cos \angle OAD}=\dfrac{d}{2\cos\frac{\alpha}{2}}=\dfrac{d}{2\cos\frac{\alpha}{2}}$

Площадь ромба равна S = a*h, с другой стороны: S = a²*sinα, приравнивая площади, получим h = a * sin α, где а - сторона ромба.

$\tt h=AD\cdot\sin\alpha=\dfrac{d\sin\alpha}{2\cos\frac{\alpha}{2}}$ - высота ромба.

Высота ромба является диаметром вписанной окружности в ромб, тогда радиус вписанной окружности равен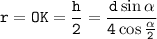 $\tt r=OK=\dfrac{h}{2}=\dfrac{d\sin\alpha}{4\cos\frac{\alpha}{2}}$

Рассмотрим теперь прямоугольный треугольник SOK и найдем в нем SK - апофему пирамиды: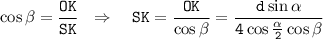 $\tt \cos \beta=\dfrac{OK}{SK}~~\Rightarrow~~~ SK=\dfrac{OK}{\cos \beta}=\dfrac{d\sin\alpha}{4\cos\frac{\alpha}{2}\cos\beta}$

Найдем теперь площадь боковой поверхности пирамиды

$\tt S_{bok}=\dfrac{1}{2}\cdot P_{OCH}\cdot SK=\dfrac{1}{2}\cdot 4\cdot\dfrac{d}{2\cos\frac{\alpha}{2}}\cdot\dfrac{d\sin\alpha}{4\cos\frac{\alpha}{2}\cos\beta}=\dfrac{2d^2tg\frac{\alpha}{2}}{\cos\beta}$