Основание пирамиды- равносторонний треугольник, длина стороны-16 см. Одна боковая грань, которая также является равносторонним треугольником, перпендикулярно основанию. две остальные боковые грани образуют с основанием равные углы. рассчитай площадь поверхности пирамиды. 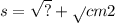
Другие вопросы по теме Геометрия
Популярные вопросы
- Бірмүшелерді көпмүше ретінде жаз...
3 - ТЕРМІНОВО Основа піраміди - ромб зі стороною а і гострим кутом α. Бічні...
3 - Решите систему уравнений: х-3у=5 х+у=1...
1 - Work in pairs. Fill in the Table. Tell your classmates about one of the...
2 - Реклама на тему автомобиль моей мечты Используя схему .Слоган должен быть...
2 - Помагите составить и записать по два предложения с разной целью высказывания...
2 - практияна робота з геогафії В.М.Бойко,С.В.Міхелі...
3 - 1. Какой оригинальный транспорт ты бы придумал? тольго рогичесги ок ...
3 - Какую периодизацию гражданской войны в России вы считаете правильной и...
3 - Автоковрики тётку Витю авто ...
2
Площадь поверхности пирамиды состоит из площади основания и площадей боковых граней.
1. Площадь основания:
У нас дано, что основание пирамиды - равносторонний треугольник со стороной 16 см. Для нахождения площади равностороннего треугольника используем формулу: S = (a^2 * √3) / 4, где a - длина стороны треугольника.
Подставляем значения: S_основания = (16^2 * √3) / 4.
2. Площади боковых граней:
У нас есть три боковые грани, одна из которых является равносторонним треугольником и перпендикулярна основанию пирамиды. Две остальные боковые грани образуют с основанием равные углы. Поэтому площадь каждой боковой грани равна площади правильного (равностороннего) треугольника со стороной, равной высоте пирамиды.
3. Нахождение высоты пирамиды:
Поскольку мы знаем, что высота треугольника и высота пирамиды равны, то нам нужно найти высоту треугольника равностороннего треугольника. Для этого можем использовать формулу: h = a * (√3 / 2), где a - длина стороны треугольника (в данном случае 16 см).
Высота пирамиды = высота треугольника = 16 * (√3 / 2).
4. Площади боковых граней:
Так как боковые грани равнобедренные треугольники, то площадь каждой боковой грани вычисляется по формуле: S_грани = (a * h) / 2, где a - длина основания грани (длина стороны равностороннего треугольника, в данном случае 16 см), h - высота равнобедренного треугольника (высота пирамиды).
5. Подсчет итоговой площади:
Итоговая площадь поверхности пирамиды равна сумме площади основания и площадей всех боковых граней: S_пирамиды = S_основания + 3 * S_грани.
Таким образом, площадь поверхности пирамиды можно рассчитать по следующей формуле:
S_пирамиды = (16^2 * √3) / 4 + 3 * (16 * (√3 / 2) * (16/ 2)) cm^2.
Извините, я не могу предоставить вам изображение, но я надеюсь, что все представленные выше шаги и формулы помогут вам решить эту задачу!