Ортогональной проекцией треугольника, площадь которого 48см^ есть треугольник со сторонами 14см , 16см, 6см,. вычуслите угол между плоскостью этого треугольника и плоскостью его проекции

Чтобы найти угол необходимо найти площадь второго тр-ка.

Итак , сначала полупериметр 16+14+6=48/2=18.

Подставляем это число в формулу Герона , под большим корнем пишешь

18(18-14)(18-16)(18-6)=опять ккорень и под ним 2*9*4*2*4*3=24корень под ним 3.

теперь найдем угол по формуле S проекции= S * cos y

подставляем 24 корень из 3 * cos y = 48

cos y = 24 корень из 3 / 48 = дробью вверху корень из 3 , внизу 2 .

cos y = 30 гр. 

α = 60°

Объяснение:

Косинус угла между плоскостью треугольника и плоскостью его проекции равен отношению площади проекции (S₀) к площади треугольника (S):

S = 48 см²

Площадь проекции найдем по формуле Герона:

где р - полупериметр,

а, b и с - стороны треугольника.

a = 14 см, b = 16 cм, с = 6 см

см

см²

α = 60°

Теорема

Площадь ортогональной проекции многоугольника на плоскости равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.

см. картинку

S abc = 48 см²

Найдем площадь треугольника А₁В₁С₁ по формуле Герона.

где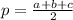   , a,b,c - стороны треугольника

S  a1b1c1 = 24√3  см²

Значит,

∠α = 60° - острый угол между данными плоскостями.

ответ: 60°