Определите, является ли отрезок AB диаметром окружности x²+6x+y²=0, если (на фото)
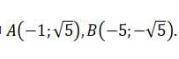
Другие вопросы по теме Геометрия
Популярные вопросы
- Периметр равнобедренного треугольника равен 84 см найдите стороны...
3 - Указать части речи.сильный втер внезапно загудел в выш..не,дерев..я...
2 - 1.әлемдегі ең үлкен кітапхана туралы не білесің? 2.қазақстанның...
3 - Переведите смешаные числа к наименьшему общему знаменателю 2 целых...
2 - 2экскаватора вырыли 840 м.первый вырыл на 40% больше чем второй.сколько...
3 - Составить предложения со слова прибор...
3 - Поставь сущ в нужном падеже.выдели окончания.укажи скл и падеж?...
3 - Что больше шесть дней 12: 00 60 секунд или 150 часов 90 секунд...
2 - Выполнить синтаксический разбор предложения: растения радуются новому...
2 - Поезд массой 10^6 кг за 1 минуту 40 секунд увеличил скорость 54...
3
Определите, является ли отрезок AB диаметром окружности x²+6x+y²=0, если А(-1 ;√5) , В(-5 ;-√5).
Объяснение:
1) Преобразуем уравнение окружности (выделим полные квадраты, если это возможно) : x²+6x+y²=0 , x²+6x+9-9+y²=0,
(х+3)²+у²=9, (х+3)²+у²=3² . Центр имеет координаты О(-3 ;0) , r=3.
2) Если АВ-диаметр , то
А и В принадлежат окружности ( координаты удовлетворяют уравнению окружности) :для А(-1 ;√5) → (-1)²+6*(-1)+√5²=1-6+5=0, 0=0 , лежит на окружности;
для В(-5 ;-√5)→ (-5)²+6*(-5)+(-√5)²= 25-30+5=0, 0=0 ,
лежит на окружности;
расстояние между А и О равно 3 : АО=√( (-3+1)²+(0+√5)²)=√( 4+5)=3Все условия выполнены, значит АВ-диаметр окружности x²+6x+y²=0.