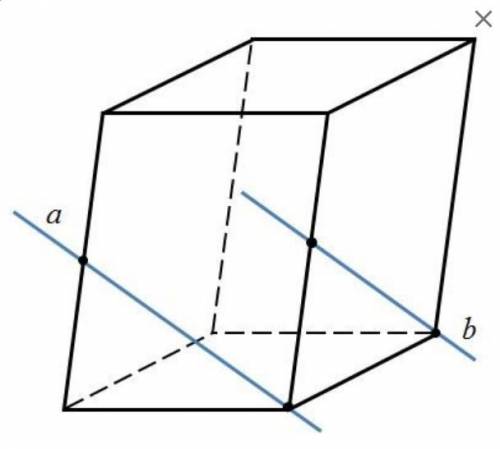
Определите взаимное расположение прямых а и b. 1) a и b – пересекающиеся прямые
2) a и b – скрещивающиеся прямые
3) a и b – параллельные прямые

Прямые a и b скрещивающиеся так как прямая a пересекает плоскость в которой находится прямая b

Объяснение:

Для определения взаимного расположения прямых a и b, сначала необходимо проанализировать угловые отношения между ними.

На данной картинке видно, что прямые a и b пересекаются в точке O. Это означает, что они имеют общую точку пересечения и являются пересекающимися прямыми. В данном случае, пересечение прямых a и b образует угол, который является острым углом, так как его мера меньше 90 градусов.

Таким образом, ответ на вопрос состоит в следующем:
1) Прямые a и b – пересекающиеся прямые, их пересечение образует острый угол.

Для более точного определения типа взаимного расположения прямых a и b, также можно воспользоваться свойствами параллельных и скрещивающихся прямых.

Параллельные прямые находятся в одной плоскости, и их расстояние между собой на протяжении всей прямой одинаково. Если бы прямые a и b были параллельными, их расстояние между собой не изменилось бы ни в одной точке. На данной картинке видно, что прямые a и b сближаются, а затем снова удаляются друг от другу. Поэтому прямые a и b не являются параллельными.

Скрещивающиеся прямые имеют общую точку пересечения и образуют два угла. На данной картинке видно, что прямые a и b пересекаются в точке O и образуют один острый угол. Скрещивающиеся прямые, также называемые пересекающимися прямыми, имеют одну общую точку пересечения и образуют острый угол. Таким образом, прямые a и b можно также назвать скрещивающимися прямыми.

В итоге, ответ на вопрос будет таким:
1) Прямые a и b – пересекающиеся прямые, их пересечение образует острый угол.
2) Прямые a и b – скрещивающиеся прямые, их пересечение образует острый угол.
3) Прямые a и b не являются параллельными прямыми.