Определите взаимное расположение прямой и плоскости 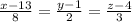
и
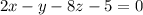
Другие вопросы по теме Геометрия
Популярные вопросы
- Написать рассказ о новорожденной звезде и дайте имя звезде....
2 - Что такое изобретение? Чем отличается научное открытие от изобретения? Для...
3 - Батарея (позывной «Или») развернута в БП. Командир батареи обнаружил Цель 21,...
1 - Просклонять по септік слово Тымақ, Құрақкөрпе НУЖНО ...
2 - В какой последовательности следующая информация встречается в тексте? 1) Бегу,...
2 - Расположи последовательно пункты алгоритма построения окружности с центром...
3 - Географія 6 клас.Користуватися атласо загальної географії 6 клас...
1 - Қазақстанның көрікті жерлерінің бірі мемлекет қайраткеріҚорықта аң құс, шөп,...
1 - Написать имена ханов, при которых: 1.Его потомкам принадлежала верховная власть...
2 - Изучив параграф заполни таблицу Основные загрязнителиКак загрязняют окружающую...
1
Первым шагом необходимо выразить параметрически уравнения для прямой и плоскости. Для прямой уравнение уже дано в параметрическом виде:
Для плоскости вначале перепишем уравнение в общем виде:
Подробнее:
1. Для прямой у нас есть три уравнения, которые связывают координаты точки на прямой:
Здесь t - параметр, полагаем его равным k.
2. Теперь выразим переменные x, y и z через t:
x = 13 + 8k
y = 1 + 2k
z = 4 + 3k
3. Подставим выражения для x, y и z в уравнение плоскости и получим выражение для k:
2(13 + 8k) - (1 + 2k) - 8(4 + 3k) - 5 = 0
26 + 16k - 1 - 2k - 32 - 24k - 5 = 0
14k - 12 = 0
14k = 12
k = 12/14
k = 6/7
4. Итак, мы получили значение параметра k. Подставим его обратно в выражения для x, y и z, чтобы получить точку пересечения прямой с плоскостью:
x = 13 + 8(6/7) = 13 + 48/7 = 91/7
y = 1 + 2(6/7) = 1 + 12/7 = 19/7
z = 4 + 3(6/7) = 4 + 18/7 = 46/7
5. Таким образом, точка пересечения прямой и плоскости имеет координаты (91/7, 19/7, 46/7).
Теперь рассмотрим взаимное расположение:
Прямая и плоскость либо могут не иметь общих точек, либо иметь одну общую точку (пересекаться между собой). Вычислив точку, мы убедились, что она существует, то есть прямая и плоскость действительно пересекаются.
Ответ: Прямая и плоскость пересекаются и имеют одну общую точку (91/7, 19/7, 46/7).