Определите острые углы прямоугольного треугольника, длины сторон которого образуют геометрическую прогрессию
Другие вопросы по теме Геометрия
Популярные вопросы
- Доброе утро решить задачу по физике 8 класс На що піде більше енергії:...
2 - пож решить Найди значение выражения, если ab = 5. ((–3a) ∙ 1,5)...
1 - В параллелограмме KMNP проведена биссектриса угла K,которая пересекает...
3 - В равнобедренном треугольнике ABCс основанием AC боковые стороны...
1 - 207 Спишите слова, вставляя пропущенные буквы. Обозначьте приставіСоставьте...
1 - Преобразуй дроб 2/4 в виде процентов...
2 - 4. Найти множество значений функции: 1) =6+3 2) =3sinx - 2...
3 - Решите уравнения: х^2-5х+6=0 х^2-6х+9=0 (3х)^2-4х+5=0 ...
2 - Объяснить графически постановку тире или его отсутствие. 1. Конец...
2 - с объяснением! Упражнение 81. Какое количество теплоты нужно передать...
2
ответ: 38° и 52°
Объяснение: в листке решение биквадратного уравнения
1. Стороны должны составить геометрическую составить геометрическую прогрессию. Пусть q >1 - знаменатель прогрессии
Тогда катет- а, другой катет - qa гипотенуза q²a
Это должно подчиняться теореме Пифагора
a² +q²a² = q⁴a² Здесь а сокращается (это говорит о том, что выбор длины первого катета на имеет значения и таких треугольников бесконечное множество) и получаем биквадратное уравнение.
q⁴ - q - 1 = 0 Я считаю, что человек, которому дают такие задания достаточно продвинут и умеет решать биквадратные уравнения. Лень писать, поэтому сразу решение.Если возьмем
сторону а равной 1, то второй катет равен
q =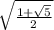 а гипотенуза
а гипотенуза
q² =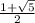
Тогда угол sinα = 1/q =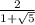 = 0.618 Это в в принципе решение, но все же найдем угол
= 0.618 Это в в принципе решение, но все же найдем угол
α = arksin(0,618) = 38°
Тогда второй угол 90°-38° = 52°