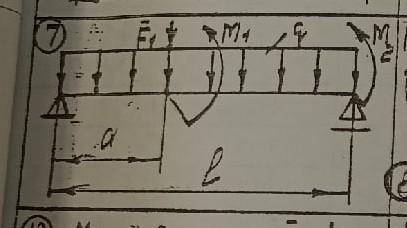
Определить реакции опор балки. Дано:
F1=18 kH
F2= —
q=2,5 kH/м
M1=17 kH•м
M2=19 kH•м
а=2 м
в=—
l = 8 м

Для определения реакций опор балки, мы можем использовать условие равновесия. В данном случае, мы рассмотрим балку в целом, и уравновешивание моментов и сил.

Уравнение равновесия моментов:
ΣM = 0

Уравнение равновесия сил по горизонтали:
ΣF_x = 0

Уравнение равновесия сил по вертикали:
ΣF_y = 0

Перейдем к решению шаг за шагом:

1. Уравнение равновесия моментов:
ΣM = 0
M1 - R1 * a + F1 * (l-a) - F2 * l + M2 = 0

Заметим, что у нас две неизвестных R1 и F2. Для решения данной системы уравнений нам понадобится еще одно уравнение равновесия. Для этого обратимся к уравнению равновесия сил по вертикали.

2. Уравнение равновесия сил по вертикали:
ΣF_y = 0
R1 + R2 - F1 = 0

Теперь у нас есть два уравнения с двумя неизвестными:
M1 - R1 * a + F1 * (l-a) - F2 * l + M2 = 0 (1)
R1 + R2 - F1 = 0 (2)

Теперь подставим известные значения в уравнение (1):
17 kH•м - R1 * 2 м + 18 kH * (8 м - 2 м) - F2 * 8 м + 19 kH•м = 0

Упростим это уравнение:
-2R1 + 144 kH - 144 kH + 19 kH•м = 0
-2R1 + 19 kH•м = 0

Следовательно:
R1 = 9,5 kH

Теперь получим значение R2, подставив R1 в уравнение (2):
R1 + R2 - F1 = 0
9,5 kH + R2 - 18 kH = 0

Упростим это уравнение:
R2 - 8,5 kH = 0

Следовательно:
R2 = 8,5 kH

Таким образом, реакция опор балки равна:
R1 = 9,5 kH
R2 = 8,5 kH

Это основное решение этой задачи. Пожалуйста, дайте знать, если вам нужно дополнительное пояснение или решение.