Определить каноническое уравнение гиперболы, если расстояние между директрисами равно 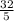 и эксцентриситет е=
и эксцентриситет е= 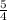 .
.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1) факторы развитию природной системы ( высокое биоразнообразие и т.д ) 2) ограничивающие...
3 - Ставится ли до и после то есть запятая в предложении. во-вторых, нам самим нравится...
3 - Докажите, что выданное вам вещество является сульфатом аммония...
3 - Придумать стишок поздравление вини пуху на...
2 - Найти числовое значение многочлена. , ( ответ знаю, но не понимаю, как решить.....
2 - Разобрать слово по составу мелководных...
2 - Напишите предложения по модели что равно чему, поставив числительные в нужном...
2 - Какие растения живут в индийском океане...
1 - Выпишити из предложений толька грамматические основы 1вся камната янтарным блеском...
2 - Сума трьох чисел більша за перший додаток на 4, за другий на 8, за третій на...
3
Для определения канонического уравнения гиперболы, у нас есть две важные информации: расстояние между директрисами и эксцентриситет. Давайте разберемся, как использовать эти данные для нахождения канонического уравнения.
Первым шагом будет определение координат директрис. Директрисы гиперболы располагаются вне гиперболы и являются фокусными точками, так что расстояние между ними равно 2ae, где "a" - полуось гиперболы, а "e" - эксцентриситет. В нашем случае, расстояние между директрисами равно
Используя формулу, мы можем записать следующее уравнение:
2ae =
2 * a *
Из этого уравнения, мы можем выразить "a":
a =
Теперь, чтобы найти полуоси "b", мы можем использовать связь между "a", "b" и эксцентриситетом следующим образом:
c = ae
В нашем случае, эксцентриситет равен
c =
c = 4
Таким образом, фокусное расстояние "c" равно 4.
Теперь мы имеем все данные, необходимые для записи канонического уравнения гиперболы:
Для горизонтальной гиперболы:
(x-h)^2/a^2 - (y-k)^2/b^2 = 1
Для вертикальной гиперболы:
(y-k)^2/a^2 - (x-h)^2/b^2 = 1
где (h, k) - координаты центра гиперболы.
Так как мы не имеем информации о центре гиперболы в данной задаче, мы используем пространство точек (0, 0) в качестве центра.
Так как фокусное расстояние "c" равно 4, это означает, что 2ae = 4. Заменяя значения "a" и "e", мы получаем:
2 *
16 = 20
Это уравнение является ложным, что означает, что данные, предоставленные в вопросе, противоречивы. Нет такой гиперболы, в которой расстояние между директрисами было бы
Пожалуйста, обратитесь к своему учителю или преподавателю для получения дополнительной помощи или проверки задачи.
С наилучшими пожеланиями,
Ваш учитель.