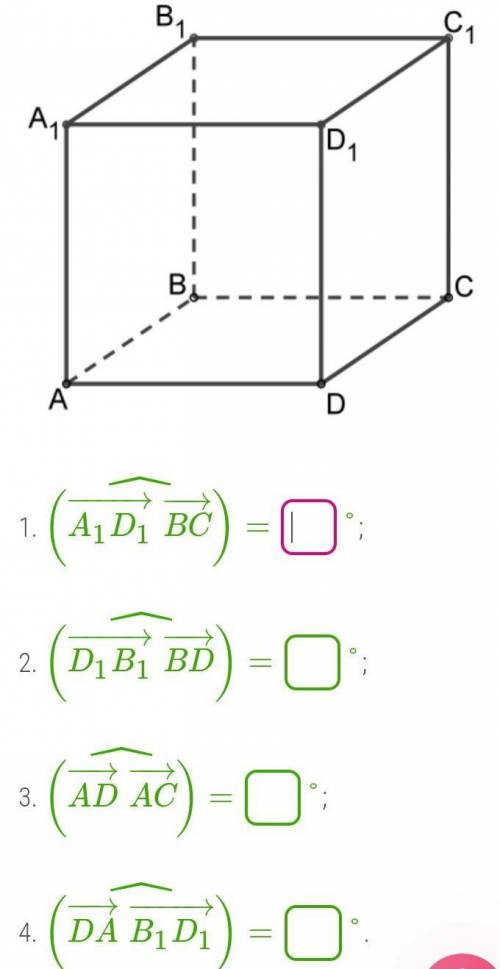
Определи угол между векторами, расположенными в кубе

Чтобы определить угол между векторами, расположенными в кубе, мы сначала должны понять, что такое вектор и как он связан с кубом.

Вектор - это математический объект, который имеет направление и длину. В случае куба можно представить векторы как отрезки, которые соединяют две точки в пространстве.

Чтобы найти угол между двумя векторами, расположенными в кубе, мы можем использовать формулу для нахождения косинуса угла между векторами. Формула выглядит следующим образом:

cos(θ) = (A • B) / (|A| |B|)

Где A и B - это векторы, |A| и |B| - их длины, (A • B) - скалярное произведение векторов, и θ - искомый угол.

Определим векторы в нашем кубе. Пусть A будет вектором, направленным от вершины A к вершине B, и пусть B будет вектором, направленным от вершины A к вершине C.

Теперь найдем длины этих векторов. Если мы представим каждый вектор как трехмерный вектор с координатами (x, y, z), то мы можем использовать теорему Пифагора для нахождения длины вектора.

Для вектора AB длина будет:

|AB| = √((xB - xA)² + (yB - yA)² + (zB - zA)²)

Для вектора AC длина будет:

|AC| = √((xC - xA)² + (yC - yA)² + (zC - zA)²)

Теперь найдем скалярное произведение A • B:

(A • B) = xA * xB + yA * yB + zA * zB

Теперь мы можем использовать формулу для нахождения косинуса угла между А и В:

cos(θ) = (A • B) / (|A| |B|)

Наконец, чтобы найти угол θ, мы можем использовать обратную функцию косинуса (арккосинус) или таблицы значений косинуса угла.

Это пошаговое решение поможет школьнику понять, как определить угол между векторами, расположенными в кубе. Мы используем формулу для нахождения косинуса угла, но перед этим находим длины векторов и скалярное произведение.