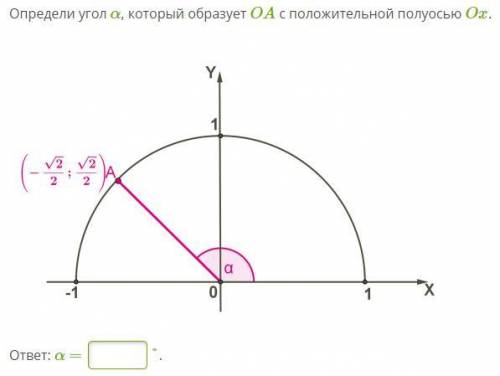
Определи угол α, который образует OA с положительной полуосью Ox.

Для определения угла α, который образует вектор OA с положительной полуосью Ox, мы должны применить тригонометрические функции.

Шаг 1: Определение координат точек O и A
На рисунке даны координаты точек O (-8, -6) и A (-2, 4), которые мы можем использовать для определения вектора OA.

Шаг 2: Вычисление разности координат
Для определения разности координат точек O и A, мы вычитаем координаты O из координат A:
OA = (x_A - x_O, y_A - y_O) = (-2 - (-8), 4 - (-6)) = (6, 10)

Шаг 3: Определение длины вектора OA
Длина вектора OA может быть вычислена с использованием формулы длины вектора:
|OA| = sqrt((x_A - x_O)^2 + (y_A - y_O)^2) = sqrt((6)^2 + (10)^2) = sqrt(36 + 100) = sqrt(136)

Шаг 4: Вычисление угла α с использованием тангенса
Угол α может быть определен с использованием формулы:
α = atan((y_A - y_O) / (x_A - x_O)) = atan(10 / 6) ≈ 59.04°

Таким образом, угол α, который образует вектор OA с положительной полуосью Ox, составляет примерно 59.04°.