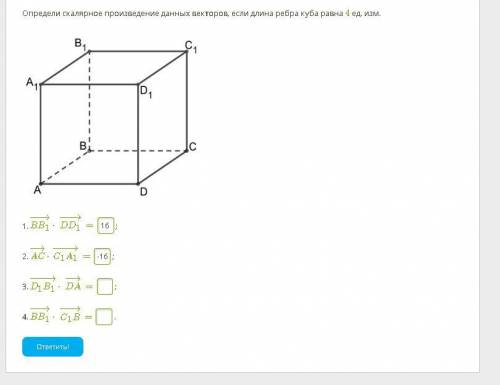
Определи скалярное произведение данных векторов, если длина ребра куба равна 4 ед. изм.
Другие вопросы по теме Геометрия
Популярные вопросы
- Может ли человек массой 75 кг поднять и удержать груз массой 85 кг при...
3 - Говорить о настоящей и ненастоящей дружбе.укажите несколько признаков...
2 - Синоним к слову растёт (в этом же падеже)...
3 - Продолжи предложения. а) изучает б) археологи ищут ! ☺...
2 - Постройте график у= |х^2-х-12| и определить: при каких значениях параметра...
2 - Представьте в виде произведения ( x-4)^2- 25x^2...
3 - Из 4 одинаковых кубиков составили фигуры изображенной на рисунке слева...
2 - Определит слово,в котором пропущена безударная проверяемая гласная корня.выпишите...
2 - Определите степень окисления na2so4, no2, p2o5, cuo, k2mno4....
1 - Это система неравенств 3-4x 19; 1+6x =13...
3
В данном случае у нас есть два вектора: AB и AD. Длина ребра куба равна 4 ед. изм., а значит, длина каждой стороны равна 4 ед. изм.
Для начала, определим координаты векторов AB и AD.
Вектор AB (прямоугольник ABCD) имеет начало в точке A(0, 0, 0) и конец в точке B(4, 0, 0). Значит, координаты вектора AB равны (4-0, 0-0, 0-0), то есть (4, 0, 0).
Вектор AD (прямоугольник ADHE) имеет начало в точке A(0, 0, 0) и конец в точке D(0, 0, 4). Значит, координаты вектора AD равны (0-0, 0-0, 4-0), то есть (0, 0, 4).
Теперь, найдем произведение соответствующих координат и сложим их.
1. Произведение x-координат: 4 × 0 = 0
2. Произведение y-координат: 0 × 0 = 0
3. Произведение z-координат: 0 × 4 = 0
Теперь сложим полученные произведения: 0 + 0 + 0 = 0.
Таким образом, скалярное произведение векторов AB и AD равно 0.
Обоснование: скалярное произведение двух векторов равно 0, если они ортогональны, то есть перпендикулярны друг другу. В данном случае, векторы AB и AD действительно ортогональны, так как их координаты вдоль координатных осей не пересекаются (скалярное произведение равно 0).
Пожалуйста, уточните, если у вас есть дополнительные вопросы.