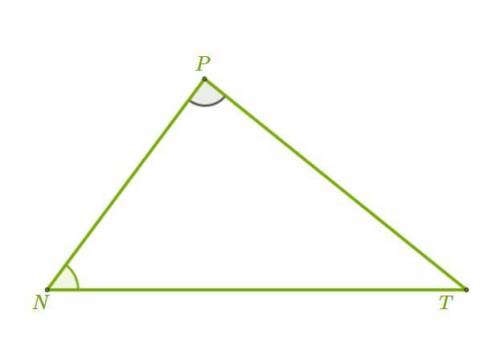
Определи площадь треугольника NPT, если NT = 11 см, ∡N=25°, ∡P=85°.
Другие вопросы по теме Геометрия
Популярные вопросы
- В чем заключается принцип соответствия?...
3 - What is your favorite celebration...
2 - Можете с заданием нужно сравнить значения выражений но с полным решением...
2 - Найдите значение выражения: 2 sin + √2 cos при = 4...
1 - ОПИСАТЬ ДЕВОЧКУ ПО АНГЛИСКИ 15 ПРЕДЛОЖЕНИЙ...
3 - От станции \(A\) до станции \(B\) поезд проехал за 1,9 часа. От станции...
1 - Хелп,товарищи,знатоки)) задача из раздела тем (дифференциальное и интегральное...
2 - Найдите предложение с прямой речью во 2-й части притчи. Составьте его...
3 - 1-тапсырма Есте сақта Ереже/правила Болжалдық сан есім бірнеше жолмен...
2 - Метанол, который является составной аспартама, заменителя сахара в напитках,...
2
Площадь треугольника = (1/2) * сторона NT * сторона PT * sin(∡NPT)
1. Начнем с определения стороны PT. У нас уже имеется сторона NT длиной 11 см и угол ∡N равный 25°. Мы можем использовать теорему синусов для определения стороны PT.
Вспомним, что теорема синусов гласит: отношение длины стороны к синусу противолежащего ей угла в треугольнике равно постоянной.
sin(∡N)/NT = sin(∡P)/PT
Заменим известные значения:
sin(25°)/11 = sin(85°)/PT
Решим это уравнение для PT. Умножим обе стороны на PT и разделим на sin(85°):
PT = (sin(85°) * 11) / sin(25°)
PT ≈ 26.75 см
2. Теперь, когда у нас есть значения для сторон NT и PT, мы можем использовать формулу площади треугольника:
Площадь треугольника = (1/2) * NT * PT * sin(∡NPT)
Заменим известные значения:
Площадь треугольника = (1/2) * 11 см * 26.75 см * sin(∡NPT)
Вычислим значение sin(∡NPT). Мы знаем, что сумма углов треугольника равна 180°, поэтому:
∡NPT = 180° - ∡N - ∡P
∡NPT = 180° - 25° - 85°
∡NPT = 70°
Заменим это значение в формуле площади треугольника:
Площадь треугольника = (1/2) * 11 см * 26.75 см * sin(70°)
Это дает нам площадь треугольника NPT. Окончательный ответ может быть вычислен, используя калькулятор или таблицы значений синуса.