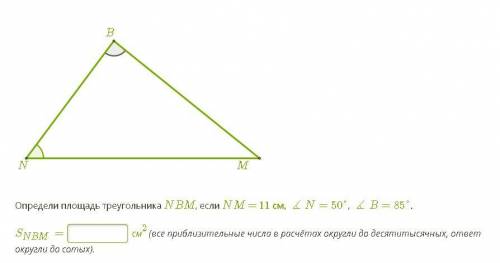
Определи площадь треугольника NBM, если NM = 11 см, ∡N=50°, ∡B=85°. SNBM= ___ см2(все приблизительные числа в расчётах округли до десятитысячных, ответ округли до сотых).
Другие вопросы по теме Геометрия
Популярные вопросы
- Рассмотри схему части речи на форзаце. назови самостоятельные части...
2 - Придумай и запиши приложения с этими словами: птица чириканью...
2 - Чему будет равна переменная «c» после выполнения этой программы: a...
3 - Какое отношение имел жилин к лошади...
3 - Влияние междоусобиц на развитие руси...
1 - 1. решите , составив уравнение: из одного пункта одновременно в разных...
2 - Мартышка сделала себе прическу 11 хвостика косичек на 3 меньше из-за...
3 - Используя основное свойство дроби, найдите значение х: 4х+1\11=50\25...
3 - 1rose eats fast fóod desn t eat meat eats sausage doesn t drink tea...
3 - 3х²-2х-=0 решите уравнение х²+3х=х²...
2
Нам дано, что сторона NM = 11 см, ∡N = 50° и ∡B = 85°. Мы можем использовать сторону NM как сторону a треугольника, а ∡N - это угол между сторонами NM и MB.
Теперь нам нужно найти сторону MB. Для этого мы можем использовать теорему синусов: a/sin(∡A) = b/sin(∡B) = c/sin(∡C), где a, b, c - стороны треугольника, ∡A, ∡B, ∡C - соответствующие углы.
Заменяя значения, которые у нас есть, мы можем найти сторону MB:
11 см / sin(50°) = MB / sin(85°).
Делим обе стороны уравнения на sin(50°) и умножаем на sin(85°):
MB = (11 см / sin(50°)) * sin(85°) ≈ 16.47 см.
Теперь у нас есть значения сторон NM (11 см), MB (около 16.47 см) и угол ∡N (50°). Мы можем использовать формулу для площади треугольника:
S = (1/2) * NM * MB * sin(∡N) ≈ (1/2) * 11 см * 16.47 см * sin(50°) ≈ (1/2) * 11 см * 16.47 см * 0.766 ≈ 67.44 см².
Итак, площадь треугольника NBM приблизительно равна 67.44 см².