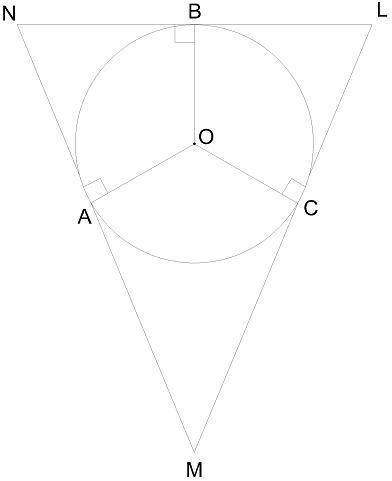
Окружность, вписанная в треугольник LMN, точками касания с треугольником делится на дуги, градусные меры которых равны: ∪AB= 93° и ∪BC= 103°.
Вычисли углы треугольника и градусную меру дуги CA.
Другие вопросы по теме Геометрия
Популярные вопросы
- Нужно найти экстремумы функции и интервалы монотонности...
3 - Найди производную функции cos⁴(5x²-1)...
2 - Тот кто ответить поставлю , Оценку и Подпишусь..Постройте предложения...
3 - Литература советского Казахстана(Достижения и пролтиворечия)...
2 - Координаты вектора в пространстве. Скалярное произведение векторов,...
2 - В солнечной хромосфере наблюдаются А)гранулы и факелы Б)пятна и факелы...
2 - РЕШИТЬ УРАВНЕНИЕ CuCl=2AlCl3=Al(OH)3=Al2(SO4 )3...
1 - ? Цена 1 единицы товара А составляет 100 руб., товара В 300 руб. Какова...
1 - Определить период полураспада радиоактивного изотопа, если 3/5 начального...
3 - Написать Эссе где вы ходите провемти лето или где вы были на каз яз...
3
Объяснение:
1.CA = 360-93-103=164
2. 1)Проведём хорды BC, AC, AB
По теореме Касательной к окружности и хорды (Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами)
Находим значение углов, которые равны, а это
LBC=LCB=UBC/2=103/2=51,5 ;
CAM=MCA =UAC/2=164/2=82;
NAB=NBA=UAB/2=93/2=46,5 ;
2) Находим углы треугольника :
NLM=BLC=180-LBC-LCB=180-103=77
NML=AMC=180-CAM-MCA=180-164=16
MNL=ANB=180-NAB-NBA=180-93=87
Проверка : 77+16+87=180 :)